About the inequality $x^{x^{x^{x^{x^x}}}} \ge \frac12 x^2 + \frac12$

Question

Problem: Let $x > 0$. Prove that $$x^{x^{x^{x^{x^x}}}} \ge \frac12 x^2 + \frac12.$$

Remark 1: The problem was posted on MSE (now closed).

Remark 2: I have a proof (see below). My proof is not nice. For example, we need to prove that $\frac{3x^2 - 3}{x^2 + 4x + 1} + \frac{12}{7} - \frac{24x^{17/12}}{7x^2 + 7} \le 0$ for all $0 < x < 1$ for which my proof is not nice.

I want to know if there are some nice proofs. Also, I want my proof reviewed for its correctness.

Any comments and solutions are welcome and appreciated.

My proof (sketch):

We split into cases:

i) $x \ge 1$:

Clearly, $x^{x^{x^{x^{x^x}}}}\ge x^x$. By Bernoulli's inequality, we have $x^x = (1 + (x - 1))^x \ge 1 + (x - 1)x = x^2 - x + 1 \ge \frac12 x^2 + \frac12$. The inequality is true.

ii) $0 < x < 1$:

It suffices to prove that $$x^{x^{x^{x^x}}}\ln x \ge \ln \frac{x^2 + 1}{2}$$ or $$x^{x^{x^{x^x}}} \le \frac{\ln \frac{x^2 + 1}{2}}{\ln x}$$ or $$x^{x^{x^x}}\ln x \le \ln \frac{\ln \frac{x^2 + 1}{2}}{\ln x}$$ or $$x^{x^{x^x}}\ge \frac{1}{\ln x}\ln \frac{\ln \frac{x^2 + 1}{2}}{\ln x}.$$

It suffices to prove that $$x^{x^{x^x}}\ge \frac{7}{12} \ge \frac{1}{\ln x}\ln \frac{\ln \frac{x^2 + 1}{2}}{\ln x}. \tag{1}$$

First, it is easy to prove that $$x^x \ge \mathrm{e}^{-1/\mathrm{e}} \ge \frac{1}{\ln x}\ln\frac{\ln\frac{7}{12}}{\ln x}.$$ Thus, the left inequality in (1) is true.

Second, let $f(x) = x^{7/12}\ln x - \ln \frac{x^2 + 1}{2}$. We have \begin{align*} f'(x) &= \frac{7}{12x^{5/12}} \left(\ln x + \frac{12}{7} - \frac{24x^{17/12}}{7x^2 + 7}\right)\\ &\le \frac{7}{12x^{5/12}} \left(\frac{3x^2 - 3}{x^2 + 4x + 1} + \frac{12}{7} - \frac{24x^{17/12}}{7x^2 + 7}\right)\\ &\le 0 \tag{2} \end{align*} where we have used $\ln x \le \frac{3x^2 - 3}{x^2 + 4x + 1}$ for all $x$ in $(0, 1]$. Also, $f(1) = 0$. Thus, $f(x) \ge 0$ for all $x$ in $(0, 1)$. Thus, the right inequality in (1) is true.
Note: For the inequality $\frac{3x^2 - 3}{x^2 + 4x + 1} + \frac{12}{7} - \frac{24x^{17/12}}{7x^2 + 7} \le 0$ for all $0 < x < 1$, we let $x = y^{12}$ and it suffices to prove that $11y^{47} + \cdots + 3 \ge 0$ (a polynomial of degree $47$, a long expression) for all $0 < y < 1$.

We are done.

Answer 1

Here, I give a full solution to the ineq given by RiverLi.
This solution has the advantage of being purely analytic. By "analytic", I mean, it is not based on any "approximate", "graphic" argument (except numeric calculations). I do try to be as clear as possible, however I do omit some explantions for some points because they're not complicated, just lengthy; in those cases, I add graphs to "justify".

---

Solution

Before going into details, I restate three simple facts we were able to easily verify by hand, and a lemma that is difficult to show.
$$x^x \ge e^{-1/e} \qquad x^{x^{x^x}}>\left(e^{-1/e}\right)^{e^{1/e}} > \underbrace{0.5877}_{=:a} \text{ and } \quad x^{x^{x^{x^{x^x}}}}> (e^{-1/e})^{1/0.587}>0.5343 $$

Lemma 1: $y \mapsto \frac{ \ln( (y+1)/2)}{\ln(y)}$ is a concave function on $(0.2,1)$.
Graph: Here
Demonstration: At the end.

Now we consider four different possible intervals of values of $x$, namely $[0,0.25)$ , $[0.25, 0.5)$, $[0.5 , 1)$ and $[1, +\infty)$ and prove the ineq in each case.

---

Case 1: When $x \ge 1$.
As @RiverLi has proven previously, $$x^{x^{x^{x^{x^x}}}} \ge x^x \ge x^2-x+1 \ge \frac{1}{2}(x^2+1)$$ Hence the inequality is true.

---

Case 2: When $x \in [0, 0.25)$, we have $$^6x> 0.534 >1/2( 0.25^2 +1) \ge \frac{1}{2}(x^2+1)$$ So this case holds.

---

Case 3: When $x \in [0.5,1)$

Consider the function $f(y)=\ln( e^y+1)$ on $(-\infty,0)$. Because its third derivative $f^{(3)}(y)=\frac{e^y(1-e^y)}{ (1+e^y)^3} $ is positive, we have the following usual inequality $$\frac{f(y)-f(z)}{y-z} \ge f'\left( \frac{y+z}{2}\right)$$ Choose $y=\ln(x^2),z=0$, we imply that: $$\frac{ \ln( (x^2+1)/2)}{\ln(x^2)} \ge \frac{x}{x+1}$$ or (note that $0<x<1$) $$\frac{x^2+1}{2} \le x^{ \frac{2x}{x+1}}$$ Besides $$^6x > x^{x^{0.5877}}= x^{ x^{0.5877}}$$ which implies the sufficiency to show $x^{0.5877} \le \frac{2x}{x+1}$, or $$2 \ge x^{0.5877} +x^{-0.4123}$$ Where the maximum of RHS on $(0.5,1)$ is easy to be analysed, which is in fact achieved at $x=1$, thus the ineq holds. See the graph here

---

Case 4 $x \in [0.25,0.5]$
As argued in the part 3, $^6x > x^{x^{0.5876}}$( I take $0.5876$ instead of $0.5877$ because it's nicer for later), it suffices to show $$\frac{\ln(x^2+1)-\ln(2)}{\ln(x)} \ge x^{0.5876}$$ on $[0.25, 0.5]$ or $$2\frac{\ln(y+1)-\ln(2)}{\ln(y)} - y^{0.2938} \ge 0$$

on $[0.5 ,\sqrt{0.5} ]\subset [0.5, 0.71]$ Indeed, we will prove the following stronger ineq after using Bernoulli's ineq,

$$2\frac{\ln(y+1)-\ln(2)}{\ln(y)}-\left( 0.6^{p} +p0.6^{p-1}(y-0.6) \right)\ge 0$$ where $p=0.2938$
Now, according to our lemma, the left fraction is concave function, which makes LHS is a summ of a concave and a linear function. Hence $LHS$ is concave. That means LHS attains minium at bord, thus $$LHS \ge \min( LHS_{|y=0.5},LHS_{|y=0.71})=0.007\dots>0$$ Graph here Hence the intial ineq holds for the interval $[0.25,0.5]$. Hence the conclusion. $\square$

---

Side note: We may not use lemma 1 for the demonstration in case 4 ( just mutiplying both side by $\ln(y)$ then analyze). However, I find this messy and tiresome to check.

----- End of solution -----------------------

---

Appendix:
Demonstration of lemma 1 I start by demonstrating another lemma
Lemma 2 $f,g$ be differentiable functions on $[a,b]$ such that $g(b)=f(b)=0$, $g(x)> 0,g'(x) < 0$ for all $a<x<b$, then if $x \mapsto \frac{f'(x)}{g'(x)}$ is an decreasing function, so is $\frac{f(x)}{g(x)}$.

Demonstration of lemma 2 Noting $h(x)= \frac{f(x)}{g(x)}$, by Cauchy's MVT, there is a number $c$ lying between $(x,b)$ such that: \begin{align}h'(x)&= \frac{f'(x)g(x)-g'(x)f(x)}{g(x)^2}\\ &=\frac{g'(x)}{g(x)}\left( \frac{f'(x)}{g'(x)}- \frac{f(x)-f(b)}{g(x)-g(b)}\right)=\underbrace{\frac{g'(x)}{g(x)}}_{<0}\underbrace{\left( \frac{f'(x)}{g'(x)}-\frac{f'(c)}{g'(c)}\right) }_{\ge 0} \le 0\end{align} Hence the conclusion.

Back to the demonstration of lemma 1
Note $h(x)=\frac{ \ln(x+1)-\ln(2)}{\ln(x)}$,it suffices to prove $h'(x)$ is decreasing. Now let's study $h$, we have: $$h'(x)= \underbrace{\left( x\ln(x)-(x+1)\ln( \frac{x+1}{2})\right)}_{=:f(x)} \frac{1}{\underbrace{x(x+1)\ln(x)^2}_{=g}}$$ (Check the formula's correctness here)
We see that $f(1)=0$, $f'(x)= \ln(x)-\ln\left( (x+1)/2\right) \le 0$. Hence we have first conclusions that $f(x) \ge 0$, $h$ increasing, and $h\le \lim_{x\rightarrow 1}h(x)=1/2$
The we have $g(1)=0$ and $$g'(x)=\ln(x)(\underbrace{2 + 2 x + \ln(x) + 2 x \ln(x)}_{ >0\text{ if } x>0.2}) \le 0$$ Besides, $$\frac{f'(x)}{g'(x)}=\frac{1-\frac{\ln(x+1)/2}{\ln(x)}}{2 + 2 x + \ln(x) + 2 x \ln(x)} =\frac{1-h(x)}{2 + 2 x + \ln(x) + 2 x \ln(x)}$$ is decreasing because the nominator is decreasing and positive ($h$ is increasing) and the denominator is increasing (by simple calculations or check graph here) Thus based on lemma 2, $h'(x)$ is decreasing. Thus conclusion $\square$

P/s: We can even prove that $y \mapsto \frac{\ln( (y+1)/2)}{\ln(y)}$ is concave on $(0,1)$, not just $( 0.2,1)$, but it is not necessary for our goal.

Answer 2

Alternative solution:

Case $0 < x < 1$:

It is easy to prove that $x^x \ge \mathrm{e}^{-1/\mathrm{e}}$. Thus, we have $$x^{x^{x^x}} \ge x^{x^{\mathrm{e}^{-1/\mathrm{e}}}}. \tag{1}$$

Also, it is easy to prove that $$\ln y - y\mathrm{e}^{-1/\mathrm{e}}\le \ln \ln \frac{12}{7}, \ \forall y > 0.$$ By letting $y = -\ln x$, we have $$x^{x^{\mathrm{e}^{-1/\mathrm{e}}}} \ge \frac{7}{12}. \tag{2}$$

From (1) and (2), we have $$x^{x^{x^x}} \ge \frac{7}{12}$$ and thus $$x^{x^{x^{x^{x^x}}}} \ge x^{x^{7/12}}.$$

It suffices to prove that $$x^{x^{7/12}} \ge \frac12 x^2 + \frac12$$ or $$x^{7/12}\ln x \ge \ln \frac{x^2 + 1}{2}.$$ Let $f(x) = x^{7/12}\ln x - \ln \frac{x^2 + 1}{2}$. We have \begin{align*} f'(x) &= \frac{7}{12x^{5/12}} \left(\ln x + \frac{12}{7} - \frac{24x^{17/12}}{7x^2 + 7}\right)\\ &\le \frac{7}{12x^{5/12}} \left(\frac{3x^2 - 3}{x^2 + 4x + 1} + \frac{12}{7} - \frac{24}{7x^2 + 7}\cdot {\frac {1189\,{x}^{2}+574\,x-35}{-35\,{x}^{2}+574\,x+1189}}\right)\\ &= {\frac { 7\left( 1-x \right) \left( 1155\,{x}^{5}-16107\,{x}^{4}-53520 \,{x}^{3}+5232\,{x}^{2}+31629\,x-9861 \right) }{12x^{5/12} \left( {x}^{2}+4\,x+1 \right) \left( 7\,{x}^{2}+7 \right) \left( -35\,{x}^{2}+574\,x+1189 \right) }}\\ &\le 0 \end{align*} where we have used $\ln x \le \frac{3x^2 - 3}{x^2 + 4x + 1}$ for all $x$ in $(0, 1]$, and $x^{17/12} \ge {\frac {1189\,{x}^{2}+574\,x-35}{-35\,{x}^{2}+574\,x+1189}}$ for all $x$ in $(0, 1)$. Also, $f(1) = 0$. Thus, we have $f(x) \ge 0$ for all $x$ in $(0, 1)$.
Note: The bounds come from the Pade approximation. For the former, just take derivative. For the latter, we only need to prove the case when ${\frac {1189\,{x}^{2}+574\,x-35}{-35\,{x}^{2}+574\,x+1189}} > 0$. Let $F(x) = \frac{17}{12}\ln x - \ln {\frac {1189\,{x}^{2}+574\,x-35}{-35\,{x}^{2}+574\,x+1189}} $. We have $$F'(x) = -{\frac { 707455\left( x-1 \right) ^{4}}{12 x \left( 1189 \,{x}^{2}+574\,x-35 \right) \left( -35\,{x}^{2}+574\,x+1189 \right) } } < 0. $$ Also, $F(1) = 0$. The desired result follows.

We are done.

Answer 3

Remarks: @Erik Satie considered $^6 x \ge \lim_{n\to \infty} {^n}x = -\frac{W(-\ln x)}{\ln x}$ for $(38/100, 1)$. I gave alternative proof of $-\frac{W(-\ln x)}{\ln x} \ge \frac12 x^2 + \frac12$ for all $x$ in $(38/100, 1)$.

---

Case $x \in (38/100, 1)$:

According to Theorem in [1] (Page 240), we have $\lim_{n\to \infty} {^n}x = -\frac{W(-\ln x)}{\ln x}$ where $W(\cdot)$ is the principal branch of the Lambert W function. Also, we have $^6 x \ge {^8}x \ge {^{10}}x \ge \cdots$ which results in $^6 x \ge \lim_{n\to \infty} {^n}x = -\frac{W(-\ln x)}{\ln x}$.

Let us prove that $-\frac{W(-\ln x)}{\ln x} \ge \frac12 x^2 + \frac12$ for all $x$ in $(38/100, 1)$.

To this end, with the substitution $x = \mathrm{e}^{-y}$ for $y\in (0, -\ln\frac{38}{100})$, we need to prove that $$\frac{W(y)}{y} \ge \frac12 \mathrm{e}^{-2y} + \frac12$$ or $$W(y) \ge \frac12 y\mathrm{e}^{-2y} + \frac12 y.$$ Since $u \mapsto u\mathrm{e}^u$ is strictly increasing on $(0, \infty)$, it suffices to prove that $$W(y)\mathrm{e}^{W(y)} \ge \left(\frac12 y\mathrm{e}^{-2y} + \frac12 y\right) \mathrm{exp}\left({\frac12 y\mathrm{e}^{-2y} + \frac12 y}\right)$$ that is $$y \ge \left(\frac12 y\mathrm{e}^{-2y} + \frac12 y\right) \mathrm{exp}\left({\frac12 y\mathrm{e}^{-2y} + \frac12 y}\right)$$ where we have used the fact $W(y)\mathrm{e}^{W(y)} = y$ for all $y > 0$.

With the substitution $z = \mathrm{e}^{-2y}$, it suffices to prove that, for all $z$ in $(38^2/100^2, 1)$, $$0 \ge \ln \frac{1 + z}{2} - \frac{1 + z}{4}\ln z.$$ The remaining is smooth.

---

Reference

[1] R. Arthur Knoebel, “Exponentials Reiterated,” The American Mathematical Monthly, No. 4, Vol. 88 (1981), pp. 235-252, Apr. 1981. https://www.maa.org/programs/maa-awards/writing-awards/exponentials-reiterated-0

Answer 4

A partial answer

---

First Fact :

For $x\in(0,1)$ we have :

$$x^{x^{x^{x^{x^{x}}}}}\geq x^{x^{x}}$$

Proof: see the Reference in my other answer .

---

Second Fact

For $x\in(0,1)$ we have :

$$ x^{x^{x}}\geq x^{\left(1+\left(x-1\right)x\right)}$$

Hint :use Bernoulli's inequality.

---

Third Fact

For $x\in[0.65,1]$ we have :

$$x^{\left(1+\left(x-1\right)x\right)}\geq b(x)=\left(x\left(1+\left(x-1\right)\cdot\left(\left(x-1\right)x\right)+0.5\left(x-1\right)^{2}\cdot\left(\left(x-1\right)x\right)\cdot\left(\left(\left(x-1\right)x\right)-1\right)\right)\right)$$

Rewrite $x^{\left(1+\left(x-1\right)x\right)}=xx^{\left(\left(x-1\right)x\right)}$ and use the binomial theorem for $p(x)=x^a$ at $x=1$ .We stop the power series at the second order .

Remains to show :

$$0.5 (x - 1)^2 (x^5 - 2 x^4 + 3 x^2 - 1)=b(x)-0.5x^2-0.5\geq0$$

Or

$$(x^5 - 2 x^4 + 3 x^2 - 1)\geq 0$$

Wich is left to the reader and easy using derivatives .

---

A lemma :

We have for $a,x\in(0,1)$:

$$x^{a^{a^{1.86a\left(1+a\left(a-1\right)\right)}}}\leq x^{a^{a^{a^{a^{a}}}}}\quad\quad(I)$$

Wich is a refinement if $x=a$

The inequality $(I)$ is equivalent to :

$$a^{a^{a}}\leq 1.86a\left(1+a\left(a-1\right)\right)$$

It seems that we have for $a\in(0.03,1)$

$$a^{a^{a}}\leq a^{0.86\left(1+\left(a-1\right)a\right)} \leq 1.87a\left(1+a\left(a-1\right)\right)$$

We start from :

$$a^{a^{a}}\leq a^{0.86\left(1+\left(a-1\right)a\right)}$$

Wich is equivalent to :

$$a^{a}\geq 0.86\left(1+\left(a-1\right)a\right)$$

The function $f(a)=a^{a}$ is convex so we have :

$$f(x)\geq f'(b)(x-b)+f(b)$$

Remains to choose judicious points wich is not hard using a graphic so I let it to the reader . Also see the reference .

Now we start from :

$$a^{0.86\left(1+\left(a-1\right)a\right)} \leq 1.87a\left(1+a\left(a-1\right)\right)$$

---

A trick is : put $a$ in exponent on both side and the inequality have the form :

$$(1.87u)^v\geq v^{0.86u}$$

The inequality in $u,v$ reminds me the inequality :

Let $a,b>0$ and $k\in(0,1)$ then we have :

$$a(1-k)+bk\geq a^{1-k}b^{k}$$

Using this we have :

$$\left(1.87u\left(x\right)\right)^{-1}\left(v\left(x\right)^{\left(\frac{x}{\left(0.86u\left(x\right)\right)}\right)^{-1}}\left(x\right)+u\left(x\right)\cdot1.87\cdot\left(1-x\right)\right)\geq \left(\left(1.87u\left(x\right)\right)^{-x}\right)x^{\left(0.86u\left(x\right)\right)}$$

Where :

$$u(x)=x\left(1+\left(x-1\right)x\right)$$ and : $$v(x)=x$$ and $x\in(0.03,1)$

---

The rest is smooth using the lemma 7.1 (p.136 see the first reference for that) .

End lemma

---

Second lemma

Let $a,x\in(0,1)$ then we have :

$$x^{a^{\frac{7}{12}}}\leq x^{a^{a^{1.87a\left(1+\left(a-1\right)a\right)}}}$$

Proof :

It's equivalent to :

$$a^{1.87a\left(1+\left(a-1\right)a\right)}\geq \frac{7}{12}$$

The function :

$$n(a)=a^{1.87a\left(1+\left(a-1\right)a\right)}$$

Is convex on $(0,1)$ so admits a global minimum on $(0,1)$. The rest is smooth again !

---

End Second lemma

Remains to show for $x,a\in(0,1)$ and $x\geq a$:

$$0.5a^{2}+0.5\leq x^{a^{\frac{7}{12}}}$$

I pursue it later thanks for advices or comments !

Reference :

Vasile Cirtoaje, "Proofs of three open inequalities with power-exponential functions", The Journal of Nonlinear Sciences and its Applications (2011), Volume: 4, Issue: 2, page 130-137. https://eudml.org/doc/223938

https://www.planetmath.org/convexfunctionslieabovetheirsupportinglines

Answer 5

Denote $$f(x,y)= x^{x^{\large y}},\quad p(x)=x^x,\quad \varphi(x)=f(x,p(x)),\quad g(x)=f(x,\varphi(x)),\tag1$$ then $$\tau_3(x)=x^{p(x)} = f(x,x),\quad\tau_4(x)=x^{\tau_3(x)} =\varphi(x),\quad \tau_5(x)=x^{\tau_4(x)}=f(x,f(x,x)),$$ and the given inequality can be reformulated as $$\tau_6(x)=g(x)\ge\dfrac{1+x^2}2.\qquad (x\in\mathbb R_+)\tag2$$

The derivatives of power towers are: $$\begin{cases} &p'(x) = p(x)(x\ln x)' = p(x)(1+\ln x) = p(x)\ln(ex),\\[4pt] &\tau'_3(x)=\tau_3(x)(p(x)\ln x)' = \dfrac1x\,\tau_3(x)p(x)(1+x\ln x\ln(ex)) = \dfrac1x\,\tau_3(x)p(x) q_3(x),\\[4pt] &\varphi'(x)=\tau'_4(x) = \tau_4(x)(\tau_3(x) \ln x)' =\dfrac1x\,\tau_4(x)\tau_3(x)(1+\ln \tau_3(x) q_3(x)),\\[4pt] &\tau'_5(x)=\dfrac1x\,\tau_5(x)\tau_4(x)(1+\ln\tau_4(x)(1+\ln\tau_3(x)q_3(x))),\\[4pt] &g'(x)=\tau'_6(x) = \dfrac1x\,\tau_6(x)\tau_5(x)(1+\tau_5(x)(1+\ln\tau_4(x)(1+\ln\tau_3(x)q_3(x)))).\\[4pt] \end{cases}\tag3$$

Also, \begin{cases} f'_y(x,y) = f(x,y) (x^y \ln x)'_y = f(x,y)x^y\ln^2x\\[4pt] f'_x(x,y) = f(x,y)(y x^{y-1}\ln x+x^{y-1})=f(x,y)x^{y-1}\ln(ex^y). \tag4\end{cases} From $(3)$ should

• $\;x_2=\operatorname{argmin} p(x)=e^{-1}\approx 0.367879,\quad \min p(x) = e^{-e^{-1}}>0.692200.\qquad\qquad(5)$

• $\;q'_3(x)=(1+x\ln x\ln(ex))' = \ln^2 x + 3\ln x +1,\;$ \begin{cases} x_{31}=\operatorname{argmax} q_3(x)= \exp \dfrac{-3-\sqrt5}2 \approx 0.072946\\ x_{32}=\operatorname{argmin} q_3(x) = \exp \dfrac{-3+\sqrt5}2 \approx 0.682518\\ q_3(x_{31})=1+(2+\sqrt5) \exp \dfrac{-3-\sqrt5}2 \approx1.309005\\ q_3(x_{32})=1+(2-\sqrt5) \exp \dfrac{-3-\sqrt5}2 \approx0.838879. \tag6\end{cases} Therefore, $\;q_3(x)\ge q_3(x_{32})\;$ and $\;\tau'_3(x)>0,\;$ wherein $\;q_3(x)\;$ increases when $\;x\in(0,x_{31})\vee(x_{32},\infty)\;$ and decreases when $\;x\in(x_{31},x_{32}).\;$

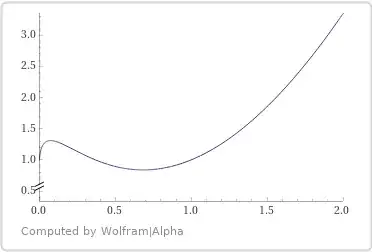
Denote \begin{cases} q_4(x)=1+q_3(x)\ln\tau_3(x),\\ q_5(x)=1+q_4(x)\ln\tau_4(x),\\ q_6(x)=1+q_5(x)\ln\tau_5(x).\tag7 \end{cases}

If $\;\underline{x\in(0,x_{31}]},\;$ then $\;q_4(x)\le 1+\ln \tau_3(x)\le\ln(ex_{31})<0,\;$
i.e. $\;\varphi(x)\;$ decreases, wherein from $(4)$ should $$g(x)=f(x,\varphi(x))\ge f(x,\varphi(x_{31})) \ge g(x_{31}) > 0.685790 > \dfrac{1+x^2}2,$$ and inequality $(2)$ holds.

If $\;x\in(x_{31},x_{2}),\;$ then both $\;q_3(x)\;$ and $\;|\ln\tau_3(x)|\;$ decrease, and $\;q_4(x)\;$ increases.

Taking in account the numerical root $\;x_4\approx 0.274689\!\dots\;$ of $\;q_4(x),\;$ easily to get $$\varphi(0.274)>0.593237,\quad \varphi'(0.274)>-0.003,$$ $$\varphi(0.275)>0.593236,\quad \varphi'(0.275)<0.0014,$$ $$x_4=\operatorname{argmin} \varphi(x) \in(0.274, 0.275),\tag8$$ $$\beta = \min \varphi(x) > \min(0.5930237-0.001\cdot 0.003, 0.593236-0.001\cdot 0.0014),$$ $$\beta = \min \varphi(x) > 0.593234.\tag9$$

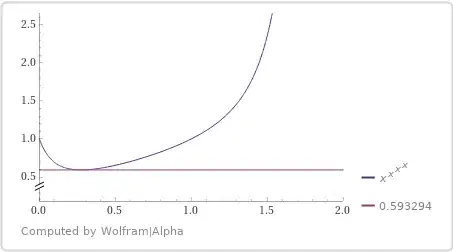
If $\;\underline{x\in(x_{31},x_4)},\;$ then

• $\;q_4(x)\in(-1.83125,0)\;$ increases,
• $\;\varphi(x)\in(0.593234,0.740040)\;$ decreases,
• $\;q_5(x)\in(1,1.551300)\;$ decreases,
• $\;|\ln\tau_5|\in(0.7658,1.9375)\;$ decreases.

Therefore, $\;q_6(x)\in(-2.006,0.235)\;$ increases.

Taking in account the numerical root $\;x_6\approx 0.225627\;$ of $\;q_6(x),\;$ easily to get

$$g(0.225)>0.5428243,\quad g'(0.225)>-0.0037,$$ $$g(0.226)>0.5428235,\quad g'(0.226)<0.0022,$$ $$x_6=\operatorname{argmin} g(x) \in(0.225, 0.226),\tag{10}$$ $$g(x) > \min(0.5428243-0.001\cdot 0.0037, 0.5428235-0.001\cdot 0.0022)>0.542820,$$ $$g(x) > \dfrac{1+0.275^2}2>\dfrac{1+x_4^2}2,$$ i.e. the inequality $(2)$ holds.

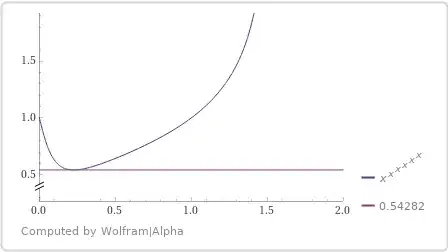
Note that $\;ex_6^\beta >1,\;$ then from $(4)$ follows increasing of $\;f(x,y)\;$ by $x$ and by $y\;$ in $\;(x_6,\infty).\;$ Since $\;\varphi(x)\;$ increases in $(x_4,x_2)$, then $\;g(x)\;$ also increases in $\;(x_4,x_2).\;$

In this way, $$g(x_4)> g(0.226) > \dfrac{1+0.291^2}2,$$ $$g(0.291) > 0.5525 > \dfrac{1+0.324^2}2,$$ $$g(0.324) > 0.5625 > \dfrac{1+0.35^2}2.$$ Therefore, inequality $(2)$ holds when $\;\underline{x\in(x_4,0.35)}.\;$

Since $\;\varphi(0.35)>0.6,\;$ then it suffices to prove the inequality $$h(x)=x^{0.6}\ln x - \ln\dfrac{1+x^2}2 \ge 0.\qquad (\underline{x\in(0.35,\infty)}).\tag{11}$$

Taking in account that $\;h(1)=0\;$ and $$h'(x)=x^{-0.4}(1+0.6 \ln x)-\dfrac{2x}{x^2+1},$$ it suffices to prove that the function $$\psi(y) = (y^5+y^{-5})(1+3\ln y)-2y^2$$ is negative when $\;y\in(0.81,1)\;$ and positive when $y>1.$

$$\textbf{Case}\;y\in(0.81,1).$$
$\;\ln y= \ln(1+y-1)=y-1-\frac12(y-1)^2+\frac13(y-1)^3-\dots\le \frac12(y-1)(3-y),\;$ $$\psi(y) \le 2+3(y-1)(3-y)-2y^2=(y-1)(7-5y) < 0.$$ Proved.

$$\textbf{Case}\;y\in(1,\infty).$$ Let $\;z=\ln y > 0,\;$ then $$\dfrac12\psi\left(e^z\right) = (3z+1)\cosh 5z - e^{2z} = \cosh 5z - \cosh 2z +3z\cosh 5z - \sinh 2z,$$ $$\dfrac12\psi\left(e^z\right) > z\sum\limits_{n=0}^\infty \left(\dfrac{3\cdot25^n}{(2n)!}-\dfrac{2\cdot 4^n}{(2n+1)!}\right)z^{2n} > 0.$$ Proved.

Therefore, inequality $(11)$ holds, and $(2)$ holds too.

Answer 6

First fact

$$ f(x)=\frac{-(W(-\ln(x)))}{(\ln(x))}= x^{x^{·^{·^·}}}$$ for $0.38<x<1$

Second fact

It seems that we have on $x\in(0.38,1)$ :

$$0.5x^{2}+0.5< f(x)< x^{x^{x^{x^{x^x}}}}\quad (I)$$

Proof for the RHS

$$x^{x^{x^{x^{x^x}}}}> ^{8}x >\cdots>f(x)$$

See https://www.maa.org/programs/maa-awards/writing-awards/exponentials-reiterated-0 .theorem p240-241.The solution is convergent for $e^{-e}<x\leq 1$ and since $e^{-e}<0.38$ wich is coherent .

Proof of the LHS

First Case

For the LHS we can substitute $x=e^y$ and multiplying by $y$.

We get:

$$0.5y(e^{2y}+1)\geq -W(-y)$$

Or :

$$-0.5y(e^{2y}+1)\leq W(-y)$$

Or :

$$0.5y(e^{2y}+1)\exp(-0.5y(e^{2y}+1))\geq y$$

Or :

$$u(y)=(\ln(0.5(e^{2y}+1))+(-0.5y(e^{2y}+1)))\leq 0$$

The derivative is :

$$u'(y)= -0.5 (e^{2 y} + 1) - e^{2 y} y + \frac{2 e^{2 y}}{e^{2 y)} + 1}$$

Lemma $x\in(0,1)$:

$$0.5\left(x-\frac{1}{\left(x\right)}\right)\leq\ln(x)$$

the proof is not hard .

Now starting with the substitution $x=e^y$ and by the lemma we have :

$$-0.5 (x^2 + 1) - x^2 \ln(x) + \frac{2 x^2}{x^2+ 1}\leq -0.5(x^{2}+1)-x^{2}\left(\left(x-\frac{1}{x}\right)0.5\right)+\frac{2x^{2}}{x^{2}+1}$$

We get a polynomial with a root in $x=1$ .Remains to evaluate a cubic polynomial wich is not hard .It show the inequality for $0<x<0.54$ or $\ln(0.38)<y<\ln(0.54)$

Second case

We need to show :

$$\ln(0.5(e^{2y}+1))+(-0.5x(e^{2y}+1))\leq0$$

For that we need a lemma :

Let $-1<y<0$ then we have with $\alpha=\frac{1}{\ln(4)}$:

$$k(x)=\ln((e^{2y}+1))-e^{\left(\alpha\right)2y}\cdot\ln\left(2\right)<0$$

The proof is not hard .

Using this lemma we need to show for $y\in(-0.74,0)$:

$$m(y)=\left(e^{\left(\alpha\right)2y}\cdot\ln\left(2\right)+\ln\left(0.5\right)+(-0.5y(e^{2y}+1))\right)\leq 0$$

$m''(y)$ have only one root expressible in terms of the Lambert's function .We deduce that $m'(y)$ have two roots on $(-0.73,0]$ .Remains to evaluate the function $m(y)$ at $y=-0.73$.

All of this show the first inequality on $(0.38,1)$ wich is a hard part .

Third Case

For the other part and in the spirit of Riverli'proof we have $x\in(0,0.38]$ :

$$x^{x^{x^{x^{x^{x}}}}}> x^{x^{x^{x^{0.69}}}}> x^{x^{\frac{1}{\sqrt{\left(3\right)}}}}> \left(x^{2}+1\right)0.5$$

The LHS is equivalent to $x^x\geq e^{-e^{-1}}>0.69$ The middle inequality is equivalent to :

$$x^{x^{0.69}}\geq \frac{1}{\sqrt{3}}$$

Or :

$$\ln(y)y\geq \frac{0.69}{\sqrt{3}}$$ Where $x^{0.69}=y$

Wich is easy using the Lambert's function .

The Rhs is :

$$x^{x^{\frac{1}{\sqrt{\left(3\right)}}}}> \left(x^{2}+1\right)0.5$$

We have for $x\in(0,0.31)$:

$$x^{x^{\frac{1}{\sqrt{\left(3\right)}}}}>e^{x^2-\ln(2)}> \left(x^{2}+1\right)0.5$$

And for $x\in[0.31,0.38]$:

$$x^{x^{\frac{1}{\sqrt{\left(3\right)}}}}> 2.6^{\left(x^{2}-\frac{\ln\left(2\right)}{\ln\left(2.6\right)}\right)}> \left(x^{2}+1\right)0.5$$

Thes two last inequality are not hard using derivatives .

Bonus inequality :Let $x>0$ then we have :

$$x^{x^{x^{x^{x^{x}}}}}\geq e^{\left(\frac{\ln^{2}\left(x+1\right)}{\ln\left(2\right)}-\ln\left(2\right)\right)}\geq \left(x^{2}+1\right)0.5$$

Hope it helps !

Reference :

R. Arthur Knoebel, “Exponentials Reiterated,” The American Mathematical Monthly, No. 4, Vol. 88 (1981), pp. 235-252, Apr. 1981