Find intersections of two functions in Maple

Question

I have two functions $f$ and $g$ defined as:

$c:=x^3+x^2+x$

$d:=20\sin x^2-5$

I am trying to find the intersections of these using Maple $16$. How would I do this?

Mhenni Benghorbal · Answer 1 · 2013-06-11T23:19:08.057

1

Here is the command

fsolve( x^3+x^2-x=20*sin(x^2)-5, x=0..2 );

If you give maple the above command you will get the answer

$$ 0.4960649664. $$

Still there are other points of intersection and its your job to find them.

edited Jun 11 '13 at 23:19

answered Jun 11 '13 at 20:36

Mhenni Benghorbal

47,431

But it finds only one intersection. I would like to find all intercestions. In this example it is five. – Lukas Jun 11 '13 at 21:03
But sorry, I made a mistakes in task.
I have two functions f and g defined as:

f:=x^3+x^2-x g:=20sinx^2-5

Now it could be fine.
– Lukas Jun 11 '13 at 21:28
fsolve has an option: fsolve(eq, x, a..b). Try a..b by -3..-2,then -2..-1, then -1..0, also 0..1, at last 1..2 . – Tony Piccolo Jun 11 '13 at 22:25
@TonyPiccolo: Thanks for pointing that out. In fact, I knew about it and I wanted the OP to get started first. It seems he is new to maple. – Mhenni Benghorbal Jun 11 '13 at 23:10

score 1 · Answer 2 · answered Jun 14 '13 at 12:45

1

I think you can use this command :

f := x^3+x^2+x = 0;

g := 20*sin*x^2-5 = 0;

fsolve({f, g});

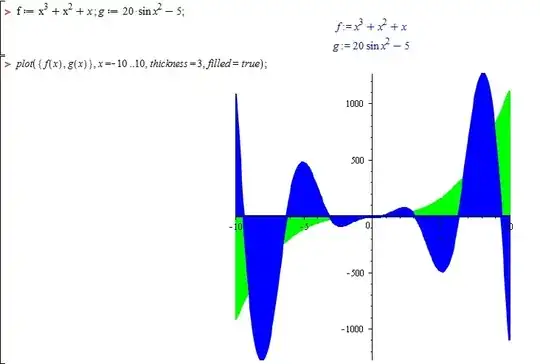
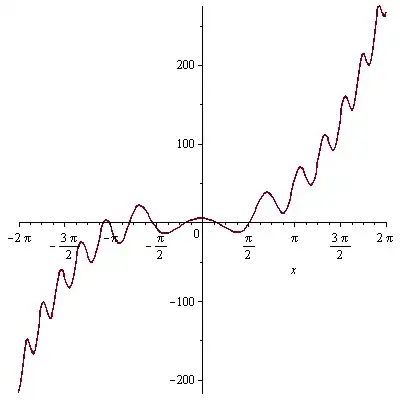
enter image description here

answered Jun 14 '13 at 12:45

Software

737

:nice attempt$\color{red}{+1}$ – M.H Jul 02 '13 at 19:56
I love the color! $\overset{+}{\uparrow}$ – amWhy Jul 22 '13 at 18:35
No, I don't think he hates you, nor does he want you to remove your account. He's just very modest/humble. That's all. I know he wants the best for all his students: and that means for you too! – amWhy Jul 22 '13 at 18:48
I know how you feel: I want everyone to be happy, too. You do not make your best teacher unhappy. I am sure of that. – amWhy Jul 22 '13 at 19:24
I am quite sure that you do not make your teacher unhappy. There is no reason for you to go away. He wants you to be happy, too. He would not want you to worry or be sad. – amWhy Jul 22 '13 at 19:47
@amwhy I wish all the best for you and for my best teacher,too. Forgive me,I'm going For sleep :) Thank you again.I'm feeling good,Now <3 – Software Jul 22 '13 at 20:36
Sleep well, @Software! ;-) – amWhy Jul 22 '13 at 20:38
@amWhy Thank you my friend ;) – Software Jul 22 '13 at 20:42
Which comment was that? – amWhy Jul 22 '13 at 20:45

score 1 · Answer 3 · answered Jul 03 '13 at 17:28

The two expressions c and d intersect at the values of x for which their difference is zero. So you can compute the roots of c-d, or plot that.

For this example it happens that all the roots fall within the default ranges of the two commands (Roots and plot) used below. For other examples you might supply additional arguments to specify the range.

c := x^3+x^2-x:

d := 20*sin(x^2)-5:

Student:-Calculus1:-Roots(c-d, numeric);

   [-3.372171392, -3.196493666, -2.489209992, -1.704885557, 

     -0.5361086923, 0.4960649664, 1.614439567]

plot(c-d);

enter image description here

Find intersections of two functions in Maple

3 Answers3