3

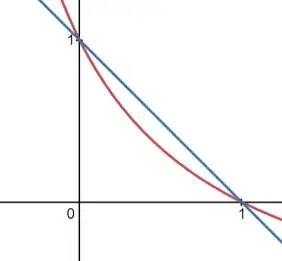
I'm starting to study triple integrals. In general, I have been doing problems which require me to sketch the projection on the $xy$ plane so I can figure out the boundaries for $x$ and $y$. For example, I had an exercise where I had to calculate the volume bound between the planes $x=0$, $y=0$, $z=0$, $x+y+z=1$ which was easy. For the projection on the $xy$ plane, I set that $z=0$, then I got $x+y=1$ which is a line.

However, now I have the following problem:

Calculate the volume bound between:

$$z=xy$$

$$x+y+z=1$$

$$z=0$$

now I know that if I put $z=0$ into the second equation I get the equation $y=1-x$ which is a line, but I also know that $z=xy$ has to play a role in the projection. If I put $xy=0$ I don't get anything useful. Can someone help me understand how these projections work and how I can apply it here?

george p
  • 113
  • $z=xy$ is same with $z=x'^2-y'^2$, only turned, called "seddle". Try to draw it you'll see projection. https://math.stackexchange.com/questions/600304/is-there-a-common-name-for-the-surface-z-xy – zkutch Jun 22 '21 at 08:19

2 Answers2

1

As you wrote plane $x+y+z=1$ cut plane $OXY$ in line $x+y=1$, which together with $x,y,z \geqslant 0$ gives triangle $$\left\lbrace\begin{array}{l}0\leqslant x \leqslant 1 \\ 0 \leqslant y \leqslant 1-x\end{array}\right\rbrace$$ Projection of intersection of $x+y+z=1$ and $z=xy$ gives $y=\frac{1-x}{1+x}$ hiperbola on plane $OXY$, which divides triangle in 2 parts. In left part plane $x+y+z=1$ is above "seddle"(Hyperbolic paraboloid) $z=xy$ and reverse on right.

Volume between plane and "seddle" from above and plane $z=0$ from below, for $x,y,z \geqslant 0$ can be calculated as $$\int\limits_{0}^{1}\int\limits_{0}^{\frac{1-x}{1+x}}\int\limits_{0}^{xy}+\int\limits_{0}^{1}\int\limits_{\frac{1-x}{1+x}}^{1-x}\int\limits_{0}^{1-x-y}$$

zkutch
  • 13,410
  • Thanks! Could you explain why are the boundaries for $z$ in both integrals different? I know that we're integrating two integrals, but when I draw the projection on paper I can't see the boundaries for $z$! – george p Jun 22 '21 at 09:37
  • In first integral $xy$ is less then $1-x-y$ i.e. saddle is below of plane, in second reverse. – zkutch Jun 22 '21 at 12:00
  • but how can I know that? – george p Jun 22 '21 at 12:26
  • As I wrote projection of intersection of $x+y+z=1$ and $z=xy$ gives $y=\frac{1-x}{1+x}$ hyperbola on plane $OXY$, which divides triangle in 2 parts. As we have equality on hyperbola, then out of hyperbola we have inequalities. Now it's easy to check which one. Write, if/when something is still unclear. – zkutch Jun 22 '21 at 16:37
1

enter image description here

The diagram that I have added is the projection in XY-plane. This curve will be the reference as we set up our integral.

As the curve in red is the projection of intersection of both surfaces in XY-plane, we equate $z$ and the equation of projection is,

$xy = 1 - x - y \implies xy + x + y = 1$

If you set up the integral in the order $dz$ first then you have to split the integral into two.

i) For $xy + x + y \leq 1, x, y \geq 0$,
$0 \leq z \leq xy$ as we are bound above by the hyperboloid.

ii) For $xy + x + y \geq 1, x + y \leq 1$,
$0 \leq z \leq 1-x-y$ as we are bound above by the plane.

Now after $dz$, you can choose either order $dx \ dy$ or $dy \ dx$. The bounds are straightforward.

But the part that I wanted to bring to your notice is that if we decide to integrate in the order $dx$ followed by $dz$ (and then $dy$ last) or in the order $dy$ followed by $dz$ (and then $dx$ last), we can set this up in one integral.

As we found, at the intersection of the plane and the hyperboloid,

$xy + x + y = 1 \implies y = \dfrac{1-x}{1+x}$

$z = xy = 1-x-y = \dfrac{x-x^2}{1+x}$

So summarizing it, for any given $x$ and $z$, you can see that $y$ is bound by hyperboloid $(\frac{z}{x})$ and the plane $(1-x-z)$ and for any given $x$, $z$ is bound by xy-plane $(z = 0)$ and the $z$ at the intersection of surfaces $\left(\frac{x-x^2}{1+x}\right)$. That leads us to the integral,

$\displaystyle \int_0^1 \int_0^{(x-x^2)/(1+x)} \int_{z/x}^{1-x-z} \ dy \ dz \ dx$

Math Lover
  • 51,819
  • Thank you very much for your extensive answer! My workbook has provided the two integral solution but you provided an even shorter one.

    When integrating by $dz$ first, how do I know that my bound for $z$ is (for example) $xy$ for the first region? I have that $x,y >0$ and $ x+y+xy=1$, but I can't see (deduce) the upper bound for $z$ from this equation! Same goes for ii)

     – george p Jun 22 '21 at 13:03
  • @georgep that is because for any $x, y$ in first quadrant below the red curve ($x+y+xy \leq1$), if you take a vertical strip (parallel to z-axis), it will touch the hyperboloid surface. But for any $x, y$ above the red curve ($x+y+xy \geq1$) (and of course $x+y\leq 1$), if you take any vertical strip, it will touch the surface of the plane. Does that clarify? – Math Lover Jun 22 '21 at 13:14