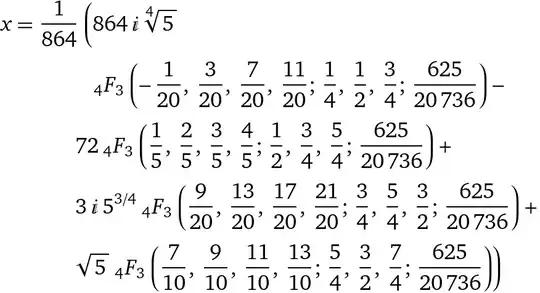5

Let $f(x) =3x^5 - 15x +5$. By Eisenstein’s Criterion we can show that $f(x)$ irreducible over $\mathbb{Q}$(Since $5 \nmid 3, 5 \vert -15,5$ and $5^2 \nmid 15$). Since $g$ is continuous and $ f( -2 ) = -61, f( -1 ) = 17 ,f( 0 ) = 5,f( 1 ) = -7,f( 2 ) = 71$. So by intermediate value theorem we can say that $f$ has three real roots. Clearly $f'(x) > 0 $ for all $x > 2$ and $f'(x) < 0$ for all $x < -2$. So $f(x)$ is monotone and so $f$ does not have zeroes in these regions. Suppose $f(x)$ has $4$ real zeroes then by using Rolle's theorem we can say that $f'(x)$ should contain at least $3$ zeroes between the roots of $f$. But $f'(x) = 15(x^4 -1)$ does not have $3$ real zeroes. So $f$ has two other complex roots. Let $K$ be the smallest subfield of complex numbers containing $\mathbb{Q}$ and $5$ roots of $f(x)$. Then using fundamental theorem of Galois theory we can say that $Gal(K/\mathbb{Q}) \approx S_5$, the symmetric group of five letters. Since $S_5$ is not solvable, by a theorem of Galois we can conclude that $f(x)$ is not solvable by radicals.

That is each zero of the polynomial $f(x)$ cannot be written as an expression involving elements of $\mathbb{Q}$ combined by the operations of addition, subtraction, multiplication, division, and extraction of roots.

How do the roots of $f$ look like? We have information about the location of real roots but I think that information may not help in finding some expression for roots. Precisely, my question is that that does there exist a series, continued fractions, or some integral which represent the roots of $f(x)$?.

Infinity_hunter
  • 5,369
  • 1
  • 10
  • 30
  • You can use Newton's method to get a series expression for a root – Andrei Jul 04 '21 at 17:30
  • Are you referring to this? If yes , can you elaborate? – Infinity_hunter Jul 04 '21 at 17:32
  • 4
    Don't know how useful it is for you, but there is a formula involving Jacobi theta function. – Jyrki Lahtonen Jul 04 '21 at 17:40
  • @Jyrki Lahtonen That is absolutely interesting!! Thanks – Infinity_hunter Jul 04 '21 at 17:42
  • 2
    Here are Bring radicals which are also a Hypergeometric function with a nice series representation that can be used to solve $x^5 +x+c=0$. Is this for a project? – Тyma Gaidash Jul 04 '21 at 17:46
  • 1
    @Tyma Gaidash This is not for a project. I was reading Galois theory and came across the above result. It is natural to ask if roots can not be expressed in terms of radicals then how else they can be expressed? – Infinity_hunter Jul 04 '21 at 18:47
  • 2
    In general this question (for degree $5$ polynomials) was answered by Klien in his seminal work Lectures on the Icosahedron and the Solution of Equations of the $5^{th}$ Degree. In particular using invariant theory Klien shows that there is a "resolvent" (called the Klien Icosahedral function) which provides a generalised idea of a radical solution to a polynomial. In fact, this question is intimately linked with the fact that for $N \leq 5$ the modular curve $X(N)$ has genus $0$. – Mummy the turkey Jul 05 '21 at 12:42
  • 2
    contd. In particular it seems that generalisations of such results are difficult for exactly this reason ($X(N)$ has genus $\geq 1$ for $N \geq 6$) and is an open problem (in the form of Hilbert's $13^{th}$ problem – Mummy the turkey Jul 05 '21 at 12:46

3 Answers3

4

It turns out one of the roots is $$x_0=\frac13 \ _4F_3\left(\frac15,\frac25,\frac35,\frac45,\frac12, \frac34,\frac54,\frac{625}{20736}\right)= 0.334166718886923432353275582781735638464962574956948610…$$ using “bring radical” link’s hypergeometric definition. Here are properties which will give you an integral, summation, and continued fraction representations here. You will have to either look up the other roots or solve for them, and derive your own values using the link. The integral representations are integrals of progressively simpler integrands of the Hypergeometric function like this:

$$x_0=\frac1{3Γ\left(\frac45\right)}\int_0^\infty \frac{\ _3F_3\left(\frac15,\frac25,\frac35,\frac12,\frac34,\frac54,\frac{625t}{20736}\right) }{e^t\sqrt[5]t}dt=\frac13\sum_0^\infty \frac{Γ(5n+1)}{405^n Γ(2(2n+1))n!}$$

sum proof.

Here are the other solutions of which I am unsure how to derive. The complex solution is also the conjugate of the one posted. Notice the similar hypergeometric arguments:

enter image description here

$$\mathop =_{\text{conjugate}}^{\text{with}}-.080931889…\pm 1.5063232344…i$$

Other real solutions:enter image description here

Top=$-1.56912279…$, Bottom=$1.39681985…$

I would write out the rest of the roots the same way and using the continued fraction formula in the Wolfram functions site link, but these are too complicated. If someone else wants to write them out, be my guest. The same goes for the nome representation. I hope this helps. Please correct me and give me feedback!

Тyma Gaidash
  • 12,081
3

There is a simple matrix representation of the root between $.33$ and $.34$ as follows:

Let $$ A =\left [ \begin{matrix} 54 & 81 & 323 & 805 & 2409\\ 18 & 27 & 108 & 269 & 805 \\ 6 & 9 & 36 & 90 & 269\\ 2 & 3 & 12 & 30 & 90\\ 1 & 1 & 4 & 10 & 30\\ \end{matrix} \right ] $$ and $$ B =\left [ \begin{matrix} 2 & 3 & 12 & 30 & 90\\ 3 & 5 & 19 & 47 & 141 \\ 6 & 9 & 35 & 87 & 261\\ 6 & 9 & 36 & 89 & 267\\ 6 & 9 & 36 & 90 & 269\\ \end{matrix} \right ] $$

Now let $C_n=AB^n$. Each of the ratios $C_n[i+1,j]/C_n[i,j]$ converges to the desired root. I suspect there are other matrices $A'$ and $B'$, independent of the pair given above, with a similar property although I am not sure yet how many such pairs there are.

Added 7/19/22:

What follows is a cheap answer to Arkady's query from the comments.

To find $A$ and $B$ proceed as follows:

First, adapt the code to solve the cubic pell found at: Units in Cube Root System to implement the algorithm to find good simultaneous approximations in dimension five found at: https://groups.google.com/g/sci.math/c/Z3qFd5IvCcs/m/GGGKxoGkkBsJ

Second, set $D_0=[1,r,r^2,r^3,r^4]$ where $r$ is the numerical value of the desired root computed to high precision.

Finally, use the code to reduce $D_0$ and produce a sequence of intermediate results $D_i$. At each step test if there is some $j<i$ s.t. $D_j=D_i$. If there is such a $j$ then $A$ and $B$ are easily computed. If not repeat.

Lots of details are missing here but hopefully you can get an idea of what I did. Not sure there are any better references than this.

O. S. Dawg
  • 217
  • This is fascinating. Could you please add how you obtained these matrices and where one might read more about them? – Arkady Jul 19 '22 at 16:45
1

The solutions are algebraic numbers. Because the Galois group of your algebraic equation isn't solvable, the solutions cannot be represented as radical expressions.

They can't be represented in terms of elementary functions either. See
closed-form expression for roots of a polynomial
Polynomials with degree $5$ solvable in elementary functions?

Additionally, your equation

$$3x^5-15x+5=0$$

is a trinomial equation. see Szabó, P. G.: On the roots of the trinomial equation. Centr. Eur. J. Operat. Res. 18 (2010) (1) 97-104

Solutions in terms of Bell polynomials or Pochhammer symbols can be obtained therefore. A closed-form solution can be obtained also using confluent Fox-Wright Function $\ _1\Psi_1$. see Belkić, D.: All the trinomial roots, their powers and logarithms from the Lambert series, Bell polynomials and Fox–Wright function: illustration for genome multiplicity in survival of irradiated cells. J. Math. Chem. 57 (2019) 59-106

IV_
  • 6,964