Circle from (2D) random walk

Question

A method is presented to create circles from sort of random walks. The $n-$gon formula is extended with a random variable.

$$x(n)=\frac{1}{n} \sum_{k=1}^{n} \cos \left( \left( X+\frac{2k}{n_{i}} \right) \pi \right) \\ y(n)=\frac{1}{n} \sum_{k=1}^{n} \sin \left( \left( Y+\frac{2k}{n_{i}} \right) \pi \right) \tag{1}$$

The total step length or "circumference" is set to $1$. Where $n$ is the number of $n-$gon edges (and steps in the random walk).

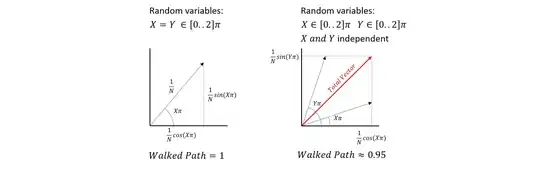
Two random (uniform distributed) variables are introduced: $X$ and $Y$. These random variables are defined as an element between: $[0,2]$ $\pi$. The number of elements is determined by variable $p$ such that:

$$p=2, \quad X \in \{0,2\} \quad \textrm{and} \quad Y \in \{0,2\}$$ $$p=3, \quad X \in \{0,1,2\} \quad \textrm{and} \quad Y \in \{0,1,2\}$$ $$p=4, \quad X \in \{0,\tfrac{2}{3},\tfrac{4}{3},2\} \quad \textrm{and} \quad Y \in \{0,\tfrac{2}{3},\tfrac{4}{3},2\}$$ $$ \quad \quad etc.$$

The effective walked path $w$ is defined as: $$w=\sum_{k=2}^{n} \sqrt{\Delta x^2_k+\Delta y^2_k}$$

Where: $\Delta x_k=x_{k}-x_{k-1}$ similar for $\Delta y_k$. Numerical the walked path for:

1. $p <4$ the effective path is measured: $w \approx 1$.
2. $p \geq 4$ the effective path is measured: $w \approx 0.96$.

Question:

Why is effective path $w \approx 0.96$ instead $1$ for random walk circles $p \geq 4$?

Observation:

When random variables $X$ and $Y$ are equal $X=Y$ (dependent) then: effective path length is: $1$ else when independent $X \neq Y$: effective path is $~0.96$.

Extra Information:

In the GIF below the circles for $p=2$ till $6$ are presented. The random walk consists of $N=1.000.000$ steps, $k$ is listed as natural numbers from: $1$ till $1.000.000$. Every walk is displayed and indexed over $n_{(i)}$.

Youtube

Basic code below (full code here Github: Github):

import numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, figsize=(12,12)) 
ax.axis('equal')
#Take steps from n=3 to [steps] to create images similar than GIF.
n=10000
steps=10000
p=4
N=np.arange(0,steps)
px=2np.random.choice(p,steps)/(p-1)
py=2np.random.choice(p,steps)/(p-1)
x=1/(steps)np.cos((px+N2/n)*np.pi)
x=np.append(x,x[0])
y=1/(steps)np.sin((py+N2/n)*np.pi)
y=np.append(y,y[0])
xc=np.cumsum(x)
yc=np.cumsum(y)
#effective walked path
xd=np.diff(xc)
yd=np.diff(yc)
dr=np.sqrt(xd2+yd2)
path=np.sum(dr)
ax.plot(xc[:steps],yc[:steps],linewidth=0.15,color='black')
plt.show()

Answer 1

The effective walked path:

The total walked path is $\bar{R}=0.96...$ (from sim.) when random variables $X$ and $Y$ are independent.

$$x(n)=\frac{1}{n} \sum_{k=1}^{n} \cos \left(X \pi \right) \\ y(n)=\frac{1}{n} \sum_{k=1}^{n} \sin \left( Y \pi \right) \tag{1}$$

Effective walked path: $$w=\sum_{k=2}^{n} \sqrt{\Delta x^2_k+\Delta y^2_k}$$

In case $X$ and $Y$ are independent: any vector start in $[0,0]$ and endpoint within the rectangle $x \in [0,1]$ and $y \in [0,1]$ is possible.

When $x$ and $y$ are uniform distributed the average vector length $\bar{R}$ can be calculated:

$$\bar{R}=\frac{1}{a^{2}}\int_{0}^{a} \int_{0}^{a} \sqrt{ x^2+y^2} \ dx dy$$

Where $a$ is the maximum step size single step. For $a=1$ I found a solution with Wolfram Alpha/Python. The total walked path would be $\bar{R}=0.765196...$ in case $x$ and $y$ are uniform distributed.

However: the angles $X$ and $Y$ are uniform distributed and not $x$ and $y$. The integral then converts to:

$$\bar{R}=\int_{0}^{1} \int_{0}^{1} \sqrt{ \cos^{2}(X \pi)+\sin^{2}(Y \pi)} \ dX dY$$

With Python (code below) and Wolfram Alpha a solution is found:

$$\bar{R}=0.958091...$$

This result for $\bar{R}$ is similar as found in simulation rand walk circles in question.

More information about this integral here: Solution integral $\;\displaystyle \iint \sqrt{\cos^2(x \pi)+\sin^2(y \pi)} \ dx\,dy$

import numpy as np
x=np.linspace(-np.pi/2,0,1001)
y=np.linspace(0,np.pi/2,1001)
X,Y =np.meshgrid(x,y)
def radius(x,y):
    return np.sqrt((np.cos(x))2+(np.sin(y))2)
z=np.array([radius(x,y) for (x,y) in zip(np.ravel(X), np.ravel(Y))])
print(np.mean(z))