1

Let $S^1 \subset \mathbb{R}^2$ be the unit circle centered at the origin and let $W\subset \mathbb{R}^2$ be the curve given by $r=\frac{\theta}{1+\theta}$ with $\theta\geq 0$.

Let $Z = S^1 \cup W \subset \mathbb{R}^2$, then Is $Z$ path connected and connected?

Here is my trial:

I know for non-empty intersection sets of (path)connected sets, their union is (path)connected. Clearly, I see $S^1$, $W$ is path-connected.(so conneced) And since $\frac{\theta}{1+\theta} \neq 1$ for all $\theta$, they are disjoint, so their union $Z$ is not (path)connected.

After @KaviRamaMurthy's comment, I realized my trial was wrong.

How to prove $Z$ is path connected or connected?

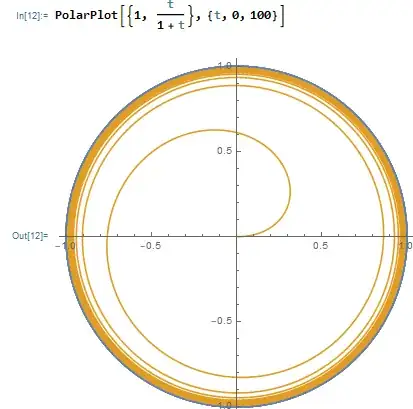
After @jasnee's comment I draw the graph of $Z$ as follows

enter image description here

It seems the graph of $r=\frac{\theta}{1+\theta}$ touches $r=1$ as $\theta \rightarrow \infty$. But except that infinity, their graph disjoint. So I guess $Z$ is not path connected, since there are no path connecting points in $S^1$ and $W$.

phy_math
  • 6,448
  • 3
    Converse a theorem is not always true. $(0,1)$ and $[1,2)$ are disjoint but their union is connected. – Kavi Rama Murthy Jul 16 '21 at 05:40
  • @KaviRamaMurthy, Ah I see. Then my proof may not be correct. I will think more carefully. – phy_math Jul 16 '21 at 05:42
  • This space seems to be connected but not path connected. I believe the standard approach to showing connectedness in such cases is to show that the only nonempty clopen set is the whole space. – themathandlanguagetutor Jul 16 '21 at 06:02
  • 1
    $\frac {2\pi n} {2\pi n+1} e^{2\pi in}$ is on the curve for any positive integer $n$. Note that any open set which contains $S^{1}$ must contain this point for large enough $n$. Conclude that the set is connected. – Kavi Rama Murthy Jul 16 '21 at 06:22
  • @Kavi Rama Murthy , can you explain in more detail, about connectedness? I understand $\frac{2\pi n}{2\pi n+1} e^{2\pi i n}$ is on the curve and any open set contains $S^1$ must contain this point for large $n$. But how this implies the set is connected? I understand the strategy explained by themathandlanguagetutor, So it seems your open set is the whole space, but I don't get this point. For example the open set of ball radius 1.01 minus ball of radius 0.9 is open set of $S^1$(am I right?) but it seems it is not open for $W$ – phy_math Jul 16 '21 at 06:47
  • The space is sometimes denoted as the topologist's whirlpool. Kavi Rama Murthy proved in his answer that it is connected. That it is not path-connected is proved here. – Paul Frost Jul 16 '21 at 08:16

1 Answers1

1

Proof of connectedness: $\frac {2\pi n} {2\pi n+1} e^{2\pi in}=\frac {2\pi n} {2\pi n+1}$ is on the curve for any positive integer $n$. Suppose you write $Z$ as a union two non-empty disjoint open sets $U$ and $V$. Then $S^{1}$, being connected, would be contained in one of these open sets, say $V$. Now $1 \in S^{1} \subset V$ , $V$ is open and $\frac {2\pi n} {1+2\pi n} \to 1$. This proves that there are points on the curve $W$ which belong to $V$. Connectedness of the curve now implies that the entire curve is contained in $V$. But this contradicts the fact that $U$ is non-empty.

Kavi Rama Murthy
  • 311,013