Finding the formula for the ulam spiral starting with $0$ as a bijective function $U:\mathbb{N}\rightarrow\mathbb{Z×Z}$

Question

$\underline{\text{Introduction}:-}$

For the last few days I've been wondering about the question below. I don't think that my approach is an elegant approach but this is the best I can do. (I am a high school student. But I have managed to gather a lot of information about advanced maths from the internet such as calculus, linear algebra, Set theory, number theory, coordinate geometry, modular arithmetic etc. So if the answer needs advanced maths then I don't have any problem, but not too advanced maths.)

Note: in this question I will include $0$ as a natural number, I know that this is rather controversial in the mathematical community but I will request not to debate about it the comment section. ($\mathbb{N}=\{0,1,2,\cdots\}$)

---

$\underline{\text{My Question}:-}$

If we put the natural numbers on the Ulam Spiral this way (Sorry I couldn't find a picture where the spiral starts at $0$, so I just put the wikipedia picture here. Just replace $n$ with $n-1$)

Then what is the formula for the cartesian coordinate on the integer lattice where each natural number lies?

---

$\underline{\text{My Attempt}:-}$

Define a bijective function $U:\mathbb{N}\rightarrow\mathbb{Z×Z}$

Where $U(n)$ gives the cartesian coordinates of $n$ on the ulam spiral.

For example:

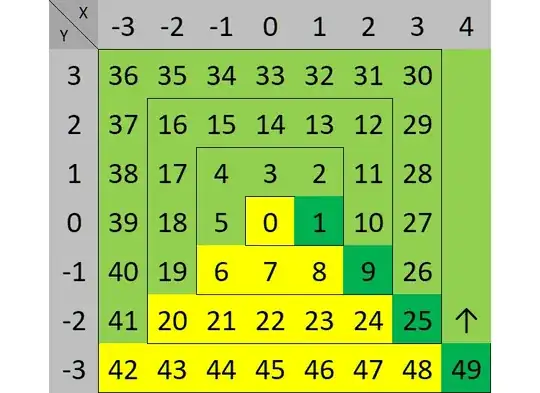
$U(0)=(0,0)$

$U(1)=(0,1)$

$U(2)=(1,1)$

$U(3)=(1,0)$

$U(4)=(1,-1)$

$\vdots$

Let, $U(n)=(x_n,y_n)$

It's obvious that how $x_n$ and $x_{n+1}$ or $y_n$ and $y_{n+1}$ would compare to each other would depend on which part of the ulam spiral $n$ is in.

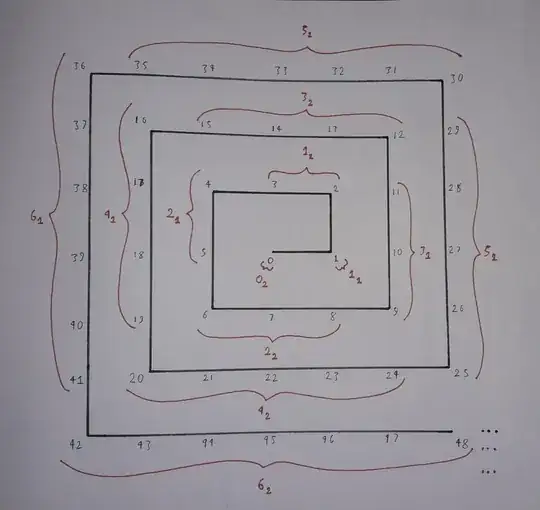
So, I divided the spiral into segments. I will denote them as $L_1$ and $L_2$ such that $|L_1|=L$ and $|L_2|=L+1$ for $L\in\mathbb{N}$ and define $0_2=\{0\}$. For example-

$0_1=\{\}=\varnothing$ $(\text{We won't consider this ever again, since it is just the null set})$

$0_2=\{0\}$

$1_1=\{1\}$

$1_2=\{2,3\}$

$2_1=\{4,5\}$

$2_2=\{6,7,8\}$

$\vdots$

So-

(Please forgive me. I cannot create pictures, so I just drew it. But I hope you understand that what $L_1$ and $L_2$ are)

Here I tried to show how each segment looks like on the spiral.

A bit of investigations gives us the result-

$\begin{align}&L_1=\{L^2,\cdots,L^2+L-1\}\\&L_2=\{(L+1)^2-(L+1),\cdots,(L+1)^2-1\}\end{align}$

For $L\in\mathbb{N}$

It's obvious that-

●If $n\in L_1$ where $L$ is odd, then $x_{n+1}=x_n$ and $y_{n+1}=y_n+1$

●If $n\in L_2$ where $L$ is odd, then $x_{n+1}=x_n-1$ and $y_{n+1}=y_n$

●If $n\in L_1$ where $L$ is even, then $x_{n+1}=x_n$ and $y_{n+1}=y_n-1$

●If $n\in L_2$ where $L$ is even, then $x_{n+1}=x_n+1$ and $y_{n+1}=y_n$

So, $$U(n+1)=\begin{cases}(x_n,y_n+1),&\text{if $n\in L_1$ and $L$ is odd}\\(x_n,y_n-1),&\text{if $n\in L_1$ and $L$ is even}\\(x_n-1,y_n),&\text{if $n\in L_2$ and $L$ is odd}\\(x_n+1,y_n),&\text{if $n\in L_2$ and $L$ is even}\end{cases}$$

If we say that, $(a,b)+(x,y)=(a+x,b+y)$

Then, $$U(n+1)=\begin{cases}(x_n,y_n)+(0,1),&\text{if $n\in L_1$ and $L$ is odd}\\(x_n,y_n)-(0,1),&\text{if $n\in L_1$ and $L$ is even}\\(x_n,y_n)-(1,0),&\text{if $n\in L_2$ and $L$ is odd}\\(x_n,y_n)+(1,0),&\text{if $n\in L_2$ and $L$ is even}\end{cases}$$

And since,

$\begin{align}&(0,1)=U(1)\\&(1,0)=U(3)\\&(x_n,y_n)=U(n)\end{align}$

We have, $$U(n+1)=\begin{cases}U(n)+U(1),&\text{if $n\in L_1$ and $L$ is odd}\\U(n)-U(1),&\text{if $n\in L_1$ and $L$ is even}\\U(n)-U(3),&\text{if $n\in L_2$ and $L$ is odd}\\U(n)+U(3),&\text{if $n\in L_2$ and $L$ is even}\end{cases}$$

This is the worst recurrence relation I have ever seen.

---

Update:

To get the formula for $L$ and whether $n\in L_1$ or $n\in L_2$, we need to solve for $L$ and $k$ in-

$\begin{cases}L^2+k=n\\1<L<n\\-L\leq k\leq L-1\end{cases}$

With a little different definition for $L_1$ and $L_2$

The definition I used here will require solving for $L$ and $k$ in

$\begin{cases}L^2+k=n\\0\leq L<n\\0\leq k\leq 2L\end{cases}$

(for more details, read this question of mine)

The solutions would be:

$$\begin{align}&L=\left\lfloor\sqrt{n}\right\rfloor\\&k=n-\left\lfloor\sqrt{n}\right\rfloor^2\end{align}$$

(For more details, read this answer to the question I linked above)

It's clear that,

If $0\leq k\leq L-1$ then $n\in L_1$

If $L\leq k\leq 2L$ then $n\in L_2$

So we can write our recurrence formula as-

$$U(n+1)=\begin{cases}U(n)+U(1)&\text{if $0\leq k\leq L-1$ and $L$ is odd}\\U(n)-U(1)&\text{if $0\leq k\leq L-1$ and $L$ is even}\\U(n)-U(3)&\text{if $L\leq k\leq 2L$ and $L$ is odd}\\U(n)+U(3)&\text{if $L\leq k\leq 2L$ and $L$ is even}\end{cases}$$

$$\begin{align}U(n+1)=&\begin{cases}U(n)+U(1),&\text{if $0\leq n-\lfloor\sqrt{n}\rfloor^2\leq\lfloor\sqrt{n}\rfloor-1$ and $\lfloor\sqrt{n}\rfloor$ is odd}\\U(n)-U(1),&\text{if $0\leq n-\lfloor\sqrt{n}\rfloor^2\leq\lfloor\sqrt{n}\rfloor-1$ and $\lfloor\sqrt{n}\rfloor$ is even}\\U(n)-U(3),&\text{if $\lfloor\sqrt{n}\rfloor\leq n-\lfloor\sqrt{n}\rfloor^2\leq 2\lfloor\sqrt{n}\rfloor$ and $\lfloor\sqrt{n}\rfloor$ is odd}\\U(n)+U(3),&\text{if $\lfloor\sqrt{n}\rfloor\leq n-\lfloor\sqrt{n}\rfloor^2\leq 2\lfloor\sqrt{n}\rfloor$ and $\lfloor\sqrt{n}\rfloor$ is even}\end{cases}\end{align}$$

It made it worse, but at least now we have the recurrence relation only in terms of $n$.

---

$\underline{\text{Some more questions}:-}$

Besides my original question in the $\text{'My Question'}$ part, I have a few more questions.

$1)$How can I get further from my recurrence relation to derive an explicit formula?

$2)$If deriving a recurrence is really not the way to approach this problem then I would request some answer to question with a different approach.

Answer 1

As the spiral is winding around, we have four $90°$ turns before completing a full rotation. Notice that each rotation starts and ends with an odd square.

This is because, starting at $r^2-1$ and adding the four sides $4(r+1)$ to complete a rotation, gives $r^2+4r+3=(r+2)^2-1$, reaching the next odd square.

Therefore, odd squares $n=(2k+1)^2$ are mapped to $(y,x)=(-k, k+1)$.

Hence, given $n$ we start by computing $k=\frac12(\sqrt{n}-1)$ to determine in which rotation the given number is located in. That is, it is located between two odd squares $(2\lfloor k\rfloor+1)^2$ and $(2\lceil k\rceil+1)^2$ that determine the start and end of the rotation.

Now we simply backtrack from the end to the start of the rotation.

Given $n$, end of rotation is at $(-K, K+1)$, where $K=\left\lceil\frac12(\sqrt{n}-1)\right\rceil$.

Given $n$, distance from the end of the rotation is $d=(2K+1)^2 - n$.

This gives $U(n)=(y,x)$ as:

$$ U(n)= \begin{cases} (-K&,+K+1-d&), & 0K+0\le d\le 2K+1\\ (-3K-1+d&,-K&), & 2K+1\lt d\le 4K+1\\ (+K&,-5K-1+d&), & 4K+1\lt d\le 6K+1\\ (+7K+1-d&,+K&), & 6K+1\lt d\lt 8K+1\\ \end{cases} $$

which is as simple as it gets.

Verifying the formula in python, gives the expected result as in the picture:

36  35  34  33  32  31  30      
37  16  15  14  13  12  29      
38  17  4   3   2   11  28      
39  18  5   0   1   10  27      
40  19  6   7   8   9   26      
41  20  21  22  23  24  25      
42  43  44  45  46  47  48  49 

Answer 2

We have the power set $\mathcal{P}(\Bbb Z \times \Bbb Z)$ and can define a transformation $\Gamma$ on the $3\text{-coordinate}$ set

$\tag 1 \mathcal U =\mathcal{P}(\Bbb Z \times \Bbb Z) \times (\Bbb Z \times \Bbb Z) \times \{-1,1\}$ by

$\quad \Gamma(S,(x,y),w))=$

$$ \begin{cases} \bigr(S \cup \{(x,y+1)\}&,(x,y+1)&,w\bigr), & w = -1 \land (x-1,y) \in S\\ \bigr(S \cup \{(x-1,y)\}&,(x-1,y)&,w\bigr), & w = -1 \land (x-1,y) \notin S \land (x-1,y-1) \in S\\ \bigr(S \cup \{(x-1,y)\}&,(x-1,y)&,-w\bigr), & w = -1 \land (x-1,y) \notin S \land (x-1,y-1) \notin S\\ \bigr(S \cup \{(x,y-1)\}&,(x,y-1)&,w\bigr), & w = 1 \land (x+1,y) \in S \\ \bigr(S \cup \{(x+1,y)\}&,(x+1,y)&,w\bigr), & w = 1 \land (x+1,y) \notin S \land (x+1,y+1) \in S\\ \bigr(S \cup \{(x+1,y)\}&,(x+1,y)&,-w\bigr), & w = 1 \land (x+1,y) \notin S \land (x+1,y+1) \notin S\\ \end{cases} $$

We have the projection mapping $\pi_2: \mathcal U \to \Bbb Z \times \Bbb Z$ onto the $2^{nd}$ coordinate.

The solution $U:\mathbb{N}\rightarrow\mathbb{Z×Z}$ is defined by

$\tag 2 U(n) = \pi_2 \circ \Gamma^{n}\big(\{(0,0)\},(0,0),1\bigr)\quad \text{for } n\ge 0$

Answer 3

Using interval notation we can partition the natural numbers by writing

$\tag 1 \Bbb N = \displaystyle \bigsqcup_{k \in \Bbb N} \bigr[k^2,(k+1)^2\bigr)$

Let $\phi_k$ denote the restriction of the $\text{counter-clockwise Ulam 0-spiral}$ function $U$ to $[k^2,(k+1)^2\bigr)$.

If $k$ is even then $$ \quad \phi_k(n)= \begin{cases} \bigr(-\frac{k}{2}, \frac{k}{2} - (n-k^2) \bigr), & k^2 \le n \le k^2 +k\\ \bigr(-\frac{k}{2}+(n-k^2-k), \frac{k}{2} -k \bigr), & k^2 + k + 1 \le n \lt (k+1)^2\\\\ \end{cases} $$

If $k$ is odd then $$ \quad \phi_k(n)= \begin{cases} \bigr(\frac{k+1}{2}, \frac{1-k}{2} + (n-k^2) \bigr), & k^2 \le n \le k^2 +k\\ \bigr(\frac{k+1}{2}-(n-k^2-k), \frac{1-k}{2} + k \bigr), & k^2 + k + 1 \le n \lt (k+1)^2\\\\ \end{cases} $$

After some deliberation we can write

$\quad U(n) =$ $$ \small{ \begin{cases} & \text{when } \lfloor \sqrt n \rfloor \text{ is even:}\\ \bigr(-\frac{\lfloor \sqrt n \rfloor}{2}, \frac{\lfloor \sqrt n \rfloor}{2} - (n-\lfloor \sqrt n \rfloor^2) \bigr), & \lfloor \sqrt n \rfloor^2 \le n \le \lfloor \sqrt n \rfloor^2 +\lfloor \sqrt n \rfloor\\ \bigr(-\frac{\lfloor \sqrt n \rfloor}{2}+(n-\lfloor \sqrt n \rfloor^2-\lfloor \sqrt n \rfloor), \frac{\lfloor \sqrt n \rfloor}{2} -\lfloor \sqrt n \rfloor \bigr), & \lfloor \sqrt n \rfloor^2 + \lfloor \sqrt n \rfloor + 1 \le n \lt (\lfloor \sqrt n \rfloor+1)^2\\\\ & \text{when } \lfloor \sqrt n \rfloor \text{ is odd:}\\ \bigr(\frac{\lfloor \sqrt n \rfloor+1}{2}, \frac{1-\lfloor \sqrt n \rfloor}{2} + (n-\lfloor \sqrt n \rfloor^2) \bigr), & \lfloor \sqrt n \rfloor^2 \le n \le \lfloor \sqrt n \rfloor^2 +\lfloor \sqrt n \rfloor\\ \bigr(\frac{\lfloor \sqrt n \rfloor+1}{2}-(n-\lfloor \sqrt n \rfloor^2-\lfloor \sqrt n \rfloor), \frac{1-\lfloor \sqrt n \rfloor}{2} + \lfloor \sqrt n \rfloor \bigr), & \lfloor \sqrt n \rfloor^2 + \lfloor \sqrt n \rfloor + 1 \le n \lt (\lfloor \sqrt n \rfloor+1)^2\\\\\end{cases} } $$