12

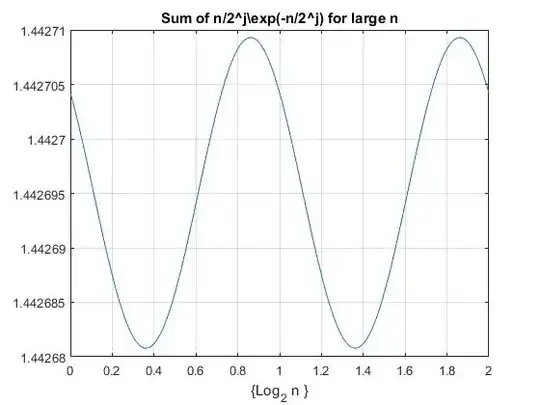
Can someone help with this sum?

Prove $$S=\lim_{n\rightarrow\infty}\sum_{k=1}^n (-1)^{k-1}{n\choose k}\frac{k}{2^k-1}=\frac{1}{\ln2}$$

I have tried to break down the $\frac{k}{2^k-1}=\sum_{j=1}^\infty \frac{k}{2^{kj}}$ and tried writing it as $$\lim_{n\rightarrow\infty}\sum_{j=1}^\infty\sum_{k=1}^n (-1)^{k-1}{n\choose k}k\left(\frac{1}{2^{j}}\right)^k,$$then using the binomial summation as such, note $\left(x=\frac{1}{2^j}\right)$ $$\lim_{n\rightarrow\infty}\sum_{j=1}^\infty\frac{1}{2^j}\frac{\mathrm{d}}{\mathrm{d}x}\left(\sum_{k=1}^n (-1)^{k-1}{n\choose k}x^{k}\right)=\lim_{n\rightarrow\infty}\sum_{j=1}^\infty\frac{n(1-x)^{n-1}}{2^j}.$$ Giving us the final sum to be $$\lim_{n\rightarrow\infty}\sum_{j=1}^\infty\frac{n\left(1-\frac{1}{2^j}\right)^{n-1}}{2^j},$$ the limit of which seems to be $0$. Which is not what we want, can someone tell me where my mistakes lie, and also point towards the solution or present it themselves. Thanks in Advance.

Blue
  • 75,673
Sarthak Sahoo
  • 336
  • The term with $2^j=n$ is around $1/e$, so you might still be on course. – Empy2 Jul 21 '21 at 14:41
  • 1
    @above ah okay wait I think the evaluation of the last sum is not 0 like I erroneously did (since i took the limit inside the summation ) but the thing is how would you compute the last sum first and then apply limits, I don't see any closed form of the last sum ?? – Sarthak Sahoo Jul 21 '21 at 15:20
  • Me neither. Are you sure it isn't a periodic function of $\ln_2 n$? – Empy2 Jul 21 '21 at 15:22
  • Where does this problem come from? – VIVID Jul 21 '21 at 15:27
  • @Empy2 as in a Fourier series or something?? Though I am pretty sure the last sum is convergent thought the ratio test. – Sarthak Sahoo Jul 21 '21 at 15:37
  • If $n=2^k$, the sum is $...8/e^8+4/e^4+2/e^2+1/e+1/2\sqrt e+...$, but if $k$ is a half-integer the sum is $...\sqrt{32}/e^{\sqrt{32}}+\sqrt8e^{\sqrt8}+...$ – Empy2 Jul 21 '21 at 15:45
  • It may be interesting to note, if you haven't already, the following integral corresponding to your sum: $$\int_0^\infty\frac 1{2^k}\left(1-\frac 1{2^k}\right)^{n-1}dk=\frac 1{n\log 2}$$ (substitute $x=1/2^k$). I find this suggestive, but I don't see how to develop a proof of the limit from it, though it might be possible to do so. – Tom Jul 23 '21 at 09:20
  • @TomWilde Yes, I had considered that since the above is just the beta integral. but am afraid this is probably just equivalent to considering an asymptotic solution as has been done below. Or equivalently using Sandwich theorem. Though I had hoped there would be a closed-form solution, but it looks though there isn't one – Sarthak Sahoo Jul 24 '21 at 17:38

2 Answers2

3

By elementary binomial coefficient relations one can derive $$S_n=\sum_{k=1}^n (-1)^{k-1} \binom{n}{k} \frac{k}{2^k-1} = n\big( a_n - a_{n-1} \big) $$ where $$ a_n =\sum_{k=1}^n (-1)^{k-1}\binom{n}{k} \frac{1}{2^k-1} $$ I've done this because I want to use an asymptotic solution I've presented to the question: Asymptotics of a recursive sequence

The first terms are simply $$ a_n \sim \frac{\log{n}}{\log{2}} + \frac{1}{2}+\frac{\gamma}{\log{2}} + \cal{o}(1) $$ Therefore, $$\lim_{n \to \infty} S_n = \lim_{n \to \infty} n \ \frac{\log{n} - \log{(n-1)} }{\log{2}} = \lim_{n \to \infty} n \, \frac{ -\log{(1-1/n)}}{\log{2}} = \frac{1}{\log{2}} $$ where a Taylor expansion has been used for the log term.

user321120
  • 6,740
2

The sum seems to vary at the fifth decimal place. I found a similar result in What's the limit of the series $\log_2(1-x)+x+x^2+x^4+x^8+\cdots$.
As I said above, in comments, the sum seems to be $$\sum_{j=1}^{\infty}\frac n{2^j}\exp\left(-\frac n{2^j}\right)$$ When $n$ is large, the dominant terms are when $2^j$ is close to $n$, then the terms in both directions (both small $j$ and large $j$) approach zero. So the sum becomes $$\sum_{k=-\infty}^{\infty} 2^{k+\log_2 n}\exp\left(-2^{k+\log_2 n}\right)$$ and the sum is the function of the fractional part of $\log_2 n$.
The graph below shows this sum varies at the fifth decimal place - the amplitude is around $0.00001426$. This is not an artifact. I took $k+\log_2n$ ranged between $-30$ and $30$. The missing terms for $k+\ln n\lt-30$ are $O(2^{-30})$, and for $k+\ln n\gt30$ are $O(\exp(-2^{30}))$.

enter image description here

Empy2
  • 50,853