1

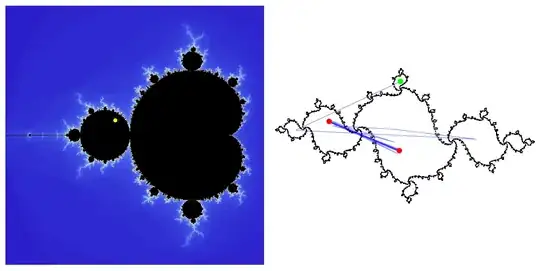
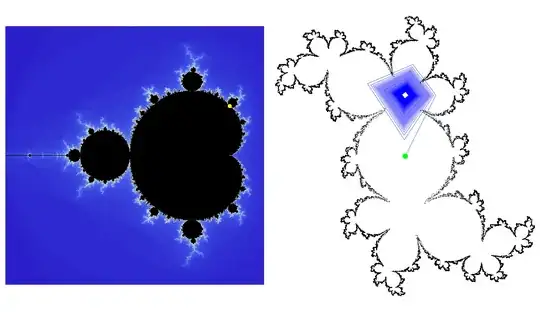
I am using the complex Mandelbrot set, with an exponent of 2 so that the iterative equation is z = z^2 + c. The escape threshold is 4.0, and the maximum number of iterations is 5000.

I find that all trajectories that belong in the set are cyclical, with the exception of a few trajectories that do not repeat during the iterations. Some of these acyclical trajectories' starting locations are:

-1, -0.25
-1, 0.25
0.25, -0.5
0.25, 0.5

Are these trajectories chaotic? Is it the acyclical nature of the trajectory that makes it chaotic?

Trajectories

Where the exponent is 4, there are also acyclical trajectories:

Trajectories2

Keep in mind that the exponent does not need to be an integer, and does not need to be positive either.

Mark McClure
  • 30,510
shawn_halayka
  • 122
  • 2
    Is the pair of scissors the only set with this apparent pattern, or are there perhaps other similar patterns with a higher iteration count maximum? If you lower the maximum, does the pattern change significantly? – abiessu Aug 01 '21 at 03:28
  • Dear abiessu, thank you for your time. I will try out your ideas. For now, I edited the question to show the acyclical trajectories where the exponent is 4. So, it's not just the standard Mandelbrot set that has acyclical trajectories. – shawn_halayka Aug 01 '21 at 03:43
  • Dear abiessu, where max iterations is 50000, there are a couple of acyclical trajectories. Where max iterations is only 500, there is a large number of acyclical trajectories. Was this what you were expecting? – shawn_halayka Aug 01 '21 at 03:55
  • 1
    If the exponent $a$ is not an integer, there is no continuous function that can reasonably be called $z^a$ for all complex numbers $z$. Any calculation will involve an artificial choice of branch cut. – Ted Aug 01 '21 at 04:34
  • Hi Ted, thanks again for your input. The pow function was given to me, for quaternions. I just dropped the last two components. As far as I can tell, the non-integer exponent works like a charm. I'm not certain what you are saying: what is a branch cut, and where does it come up in my code? https://github.com/sjhalayka/bezier_fractal_2d/blob/d017cd5db9bee462088d5eea11450277c791a3ed/main.h#L118 P.S. Thanks Ted. I kept your past suggestions in mind when asking this particular question. – shawn_halayka Aug 01 '21 at 04:39
  • 1
    In line 132 of that code, you have the term sqrtf(in.imag() * in.imag()) in the denominator, so it is undefined if in.imag() is 0. Thus the function does not work on the imaginary axis. When the exponent is not an integer, there will always be a set of points you have to exclude to get a continuous function; this is called a branch cut. There are many ways to choose a branch cut and it is arbitrary. – Ted Aug 01 '21 at 05:43
  • 1
    "imaginary axis" should be "real axis" in my comment above. – Ted Aug 01 '21 at 05:51
  • Thanks again, Ted! – shawn_halayka Aug 01 '21 at 16:01

1 Answers1

5

You have a few points of confusion that make this question (and your previous ones here and on StackOverflow) difficult to answer. Here is some clarification.

  • The Mandelbrot set lives in the context of complex dynamics, i.e. the study of the iteration of analytic functions mapping the complex plane to itself. A huge majority of MSE questions on the Mandelbrot set should tagged [complex-dynamics], rather than [fractals].

  • Given a complex analytic function, it makes no sense to refer to a single trajectory as chaotic. It might make sense to refer to the dynamics of the function itself as chaotic on some closed subset of the plane. Bob Devaney is generally credited with writing down the exact criteria that a function should satisfy to be considered chaotic a on a set.

  • The fundamental set associated with the chaotic dynamics of a complex analytic function is the Julia set. For a polynomial, the Julia set can be characterized as the closure of the set of repelling periodic points of that polynomial. To be clear, the Julia set of a function lives in the dynamical plane for that function - i.e. the plane where the iteration happens.

  • The Mandelbrot set specifically involves the iteration of functions chosen from the family $$ f_c(z) = z^2 + c, $$ where $c$ is a complex parameter. Specifically, the Mandelbrot set is defined to be the set of all complex numbers $c$ such that the Julia set of $f_c$ is connected or equivalently, such that the orbit of the critical point $z_0=0$ under iteration of $f_c$ remains bounded. In particular, the Mandelbrot set provides a general classification of the types of dynamics that arise for quadratic functions.
    Note that the the Mandelbrot set lives in the parameter ($c$) plane - not in the dynamical ($z$) plane; in particular, trajectories don't live in the Mandelbrot set.

Here's a picture that might help clarify:

enter image description here

On the left, we see the Mandelbrot set with the single point $z_0=-0.9+0.15i$ highlighted in yellow. The corresponding Julia set appears on the right, together with an orbit that starts at the green dot and is ultimately attracted to a cycle of period two indicated by the two red dots.

If we change the point, we change the dynamical picture. For example, here's the picture for your point $c=0.25+0.5i$:

enter image description here

You can play with these sorts of images on this web page.

Judging from your pictures, I would guess that you are asking about the nature of the critical orbits (i.e. the orbits from the point $z_0=0$) of the functions $f_c$ for various choices of $c$, like $c=0.25+0.5i$. My second picture above shows how I would illustrate the orbit on the Julia set for that particular value of $c$. The dynamics of $f_c$ for each of the points you list happen to be parabolic, which is a bit tricky to deal with. There have been several discussions on this site involving parabolic dynamics.

Mark McClure
  • 30,510
  • Mark, you’re just plain awesome. Thank you so much for your explanation of things. – shawn_halayka Aug 01 '21 at 16:02
  • P.S. where then does chaos emerge with regard to the Mandelbrot set? – shawn_halayka Aug 01 '21 at 16:03
  • Someone told me that calculating the Lyapunov exponent will tell me if the system is chaotic or not. I have the trajectories, I just don’t know where to start when calculating this Lyapunov exponent. Any help would be greatly appreciated. – shawn_halayka Aug 01 '21 at 16:20
  • 1
    @shawn_halayka In fact, every polynomial is chaotic on its Julia set - that's really the whole point of the Julia set. :) The function $f(z)=z^2$, for example, is chaotic on the unit circle. You can find an illustrative explanation of that fact on this web page. – Mark McClure Aug 01 '21 at 17:55
  • 1
    The Mandelbrot set does not break the $f_c$s up into chaotic vs not chaotic. Rather, it provides a classification of the types of dynamics that are possible for quadratic functions. The different components of the Mandelbrot set correspond to values of $c$ where the critical orbit of $f_c$ is attracted to periodic orbits of various lengths. The main cardioid corresponds to attractive fixed points, the large circle just to the left corresponds to orbits of period 2, and the baby-brots all correspond to higher order periods. – Mark McClure Aug 01 '21 at 18:01
  • 1
    I don't think it's common to use Lyapunov exponents in complex dynamics. While it could certainly be done, I think there's a lot of structure complex dynamics that precludes the need for Lyapunov exponents. The fact that every polynomial has a Julia set, for example, is not true for real dynamics. – Mark McClure Aug 01 '21 at 18:04
  • 1
    I implemented the code to calculate the Lyapunov exponent and it returns a negative value for trajectories in the set, and a positive value for trajectories that are not in the set. I see now that tells us nothing more than the Z complex variable’s magnitude would. – shawn_halayka Aug 03 '21 at 16:36