What does $\mathrm{Spec}(\mathbb{Z})\times_{\mathrm{Spec}(\mathbb{F}_{1})}\mathrm{Spec}(\mathbb{Z})$ look like?

Question

See also: What does $\mathrm{Spét}(H\mathbb{Z})\times_{\mathrm{Spét}(\mathbb{S})}\mathrm{Spét}(H\mathbb{Z})$ look like?.

---

$\newcommand{\F}{\mathbb{F}}\newcommand{\N}{\mathbb{N}}\newcommand{\Z}{\mathbb{Z}}$One of the most mysterious objects in mathematics is the elusive "field with one element", and coming with it is the arithmetic curve $\mathrm{Spec}(\mathbb{Z})\times_{\mathrm{Spec}(\mathbb{F}_{1})}\mathrm{Spec}(\mathbb{Z})\cong\mathrm{Spec}(\mathbb{Z}\otimes_{\mathbb{F}_{1}}\mathbb{Z})$. I want to know what such a thing would look like, and hence am trying to work it out in one particular model for geometry over $\mathbb{F}_1$, that of binoids. Here are some definitions (for the question, it suffices to know 1–3 only).

1. A binoid is a commutative monoid $M$ together with an absorbing element $0$.
2. An ideal of $M$ is a subset $I$ such that
   • $0\in I$.
   • If $a\in I$ and $r\in M$, then $ra\in I$.
3. An ideal $I$ of $M$ is prime if it is proper and whenever $ab\in I$ then $a\in I$ or $b\in I$.
4. The spectrum $\mathrm{Spec}(M)$ of a binoid $M$ is the set of all prime ideals of $M$.
5. The Zariski topology on $\mathrm{Spec}(M)$ is the topology generated by the collection $\{D(I)\}$ with $D(I)=\mathrm{Spec}(M)\setminus V(I)$, where $$V(I)=\{\mathfrak{p}\in\mathrm{Spec}(M):I\subset\mathfrak{p}\}.$$
6. A distinguished open of $\mathrm{Spec}(M)$ is a set of the form $D_f=D(\{f\})$ for some $f\in A$. These form a basis for the Zariski topology on $\mathrm{Spec}(M)$.
7. A binoidal space is a pair $(X,\mathcal{O}_X)$ with $X$ a topological space and $\mathcal{O}_X$ a sheaf of binoids on $X$.
8. An affine binoid scheme is a binoidal space of the form $(\mathrm{Spec}(M),\mathcal{O}_{M})$, where $\mathcal{O}_{M}$ is defined on the distinguished opens by $$\mathcal{O}_{M}(D_f)=M_f.$$

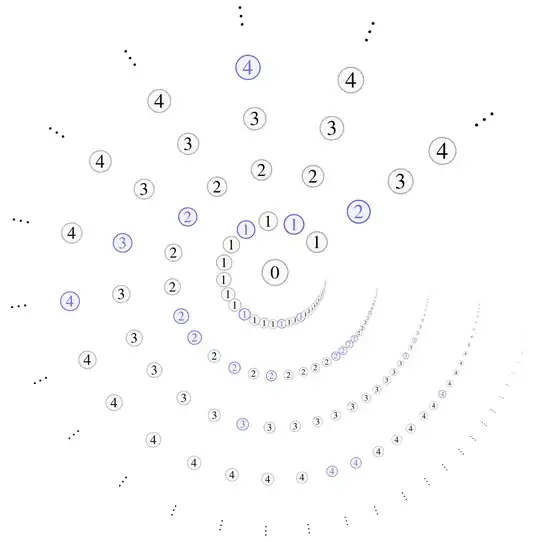
For example, every ring $R$ has an associated binoid, given by forgetting the addition of $R$. We have also a tensor product of binoids, and the tensor product $\mathbb{N}\otimes_{\mathbb{F}_{1}}\mathbb{N}$ is isomorphic to a countable direct sum of the multiplicative monoid of positive natural numbers, $(\mathbb{N}\setminus\{0\},\cdot,1)$, adjoined with an absorbing element $\{0\}$. It looks like this:

The binoid $\Z\otimes_{\F_{1}}\Z\cong(\Z\setminus\{0\},\cdot)^{\oplus{\N}}\sqcup\{0\}$ is pictured in the same way, we just add negative numbers.

What I'd like to ask is: What are the $\mathrm{Spec}$'s of the main objects involved here, including $\mathrm{Spec}(\mathbb{N})$ and $\mathrm{Spec}(\mathbb{Z})$ (where $\mathbb{N}=(\mathbb{N},\cdot,1)$ and similarly for $\mathbb{Z}$), and, above all, \begin{align*} \mathrm{Spec}(\mathbb{N})\times_{\mathrm{Spec}(\mathbb{F}_{1})}\mathrm{Spec}(\mathbb{N}) &\cong \mathrm{Spec}(\mathbb{N}\otimes_{\mathbb{F}_{1}}\mathbb{N}),\\ \mathrm{Spec}(\mathbb{Z})\times_{\mathrm{Spec}(\mathbb{F}_{1})}\mathrm{Spec}(\mathbb{Z}) &\cong \mathrm{Spec}(\mathbb{Z}\otimes_{\mathbb{F}_{1}}\mathbb{Z}), \end{align*} the sets of prime ideals of the binoids $\N\otimes_{\F_{1}}\N\cong(\N\setminus\{0\},\cdot)^{\oplus{\N}}\sqcup\{0\}$ and $\Z\otimes_{\F_{1}}\Z\cong(\Z\setminus\{0\},\cdot)^{\oplus{\N}}\sqcup\{0\}$?

Answer 1

The prime ideals of $(\mathbb{N},\cdot,1,0)$

Let $\mathbb{P}$ be the set of prime numbers. There is a bijection$^1$ $$\mathcal{P}(\mathbb{P}) \to \mathrm{Spec}_{\mathbf{CMon}_0}((\mathbb{N},\cdot,1,0)),~ E \mapsto \langle E \rangle,$$ which maps a set of prime numbers to the ideal generated by it. Explicitly, we have $\langle \emptyset \rangle = \{0\}$ and $\langle E \rangle = \bigcup_{p \in E} p\mathbb{N}$ for $E \neq \emptyset$.

Proof. With the explicit description of $\langle E \rangle$ it is easy to see that $\langle E \rangle$ is indeed a prime ideal with $E = \langle E \rangle \cap \mathbb{P}$. Let $I$ be a prime ideal and $E := I \cap \mathbb{P}$. Clearly, $\langle E \rangle \subseteq I$. Conversely, if $n \in I$, w.l.o.g. $n \neq 0$, we may factor $n$ as a product of prime numbers. Since $I$ is prime, one of the prime numbers, say $p$, must be contained in $I$. Then $p \in E$ and $n \in p\mathbb{N}$, so $n \in \langle E \rangle$. $\square$

The homomorphism $(\mathbb{N},\cdot,1,0) \hookrightarrow (\mathbb{Z},\cdot,1,0)$ induces a bijection on the spectra (you only need to check that a prime ideal $I \subseteq \mathbb{Z}$ satisfies $I = (I \cap \mathbb{N}) \cup -(I \cap \mathbb{N}$), which is easy). So we also have a bijection $\mathcal{P}(\mathbb{P}) \to \mathrm{Spec}_{\mathbf{CMon}_0}((\mathbb{Z},\cdot,1,0))$, $E \mapsto \langle E \rangle$.

Direct sums

Here is a more conceptual explanation and generalization.

Let $(M_i)_{i \in \mathbb{N}}$ be a family of commutative monoids (not with zero at this point), written multiplicatively. Their coproduct $\coprod_{i \in I} M_i$ is the "direct sum" $\bigoplus_{i \in I} M_i \subseteq \prod_{i \in I} M_i$ consisting of those tuples which are $1$ almost everywhere. The inclusions $\iota_i : M_i \hookrightarrow \bigoplus_{i \in I} M_i$ induce maps $\mathrm{Spec}_{\mathbf{CMon}}(\bigoplus_{i \in I} M_i) \to \mathrm{Spec}_{\mathbf{CMon}}(M_i)$ and hence a map $$\alpha : \mathrm{Spec}_{\mathbf{CMon}}(\bigoplus_{i \in I} M_i) \to \prod_{i \in I} \mathrm{Spec}_{\mathbf{CMon}}(M_i).$$ Conversely, given a family of prime ideals $\mathfrak{p}_i \subseteq M_i$, the ideal $\langle \bigcup_{i \in I} \mathfrak{p}_i \rangle = \bigcup_{i \in I} \langle \mathfrak{p}_i \rangle \subseteq \bigoplus_{i \in I} M_i$ is a prime ideal which restricts to the $\mathfrak{p}_i$ along $\iota_i$. If $\mathfrak{p} \subseteq \bigoplus_{i \in I} M_i$ is any prime ideal, consider some element $m = \prod_{i \in I} m_i \in \mathfrak{p}$. Since $\mathfrak{p}$ is prime, we have $m_i \in \mathfrak{p}$ for some $i$, so $m_i \in \mathfrak{p} \cap M_i$, and since $m$ is a multiple of $m_i$, we see $m \in \langle \mathfrak{p} \cap M_i \rangle$. This shows that $\alpha$ is bijective. (Actually, $\alpha$ is an isomorphism of ringed spaces.)

Adjoining a zero

Notice that for every $M \in \mathbf{CMon}$ there is a canonical bijection $$\mathrm{Spec}_{\mathbf{CMon}_0}(M \cup \{0\}) \to \mathrm{Spec}_{\mathbf{CMon}}(M),~ \mathfrak{p} \mapsto \mathfrak{p} \cap M.$$

The prime ideals of $(\mathbb{N},\cdot,1,0)$ again

The monoid $(\mathbb{N},+,0)$ has exactly two prime ideals, namely $\emptyset$ and $\mathbb{N}^+$. Prime factorization yields an isomorphism $(\mathbb{N},\cdot,1,0) \cong (\mathbb{N}^+,\cdot,1) \cup \{0\} \cong \bigl(\bigoplus_{p \in \mathbb{P}} (\mathbb{N},+,0) \bigr) \cup \{0\}$. Thus, the previous results show that $$\mathrm{Spec}_{\mathbf{CMon}_0}((\mathbb{N},\cdot,1,0)) \cong \prod_{p \in \mathbb{P}} \mathrm{Spec}_{\mathbf{CMon}}((\mathbb{N},+,0)) = \prod_{p \in \mathbb{P}} \{\emptyset,\mathbb{N}^+\} \cong \mathcal{P}(\mathbb{P}).$$

Finally, the tensor product

Now we can also compute the prime ideals of $(\mathbb{N},\cdot,1,0) \otimes_{\mathbb{F}_1} (\mathbb{N},\cdot,1,0)$. It is $(\mathbb{N}^+,\cdot,1) \otimes_{\mathbb{F}_0} (\mathbb{N}^+,\cdot,1)$ with an adjoined zero. The tensor product refers to commutative $\mathbb{F}_0$-algebras aka commutative monoids; I will just write $\otimes$ since the object themselves show which category we are in. We have $$(\mathbb{N}^+,\cdot,1) \otimes (\mathbb{N}^+,\cdot,1) \cong \bigoplus_{p,q \in \mathbb{P}} (\mathbb{N},+,0) \otimes (\mathbb{N},+,0) \cong \bigoplus_{p,q \in \mathbb{P}} (\mathbb{N},+,0)$$ and therefore $$\mathrm{Spec}_{\mathbf{CMon}}((\mathbb{N},\cdot,1,0) \otimes_{\mathbb{F}_1} (\mathbb{N},\cdot,1,0)) \cong \mathrm{Spec}_{\mathbf{CMon}}((\mathbb{N}^+,\cdot,1) \otimes (\mathbb{N}^+,\cdot,1)) \cong \mathcal{P}(\mathbb{P} \times \mathbb{P}).$$ Explicitly, the prime ideal associated to a subset $E \subseteq \mathbb{P} \times \mathbb{P}$ is $\bigcup_{(p,q) \in E} \langle p \otimes 1, 1 \otimes q \rangle$ (I think).

$^1$It is a really good idea to not forget forgetful functors in general, especially here when we need to emphasize the multiplicative structure and the zero. This is why I don't just write $\mathbb{N}$, which is merely the underlying set of the monoid with zero $(\mathbb{N},\cdot,1,0)$.

$^2$The term "binoid" is a bad choice here, I won't use it.

Answer 2

$\newcommand{\Z}{\mathbf{Z}}$Marc Hoyois pointed on a related question of mine on MathOverflow that I conflated the tensor products involved in this case. What I have been calling $\mathbf{Z}\otimes_{\mathbf{F}_{1}}\mathbf{Z}$ should have been called $\mathbf{Z}\otimes_{\mathbf{N}_{+}}\mathbf{Z}$, while what I have called $\mathbf{Z}\otimes_{\mathbf{F}_{1}}\mathbf{Z}$ is given by \begin{align*} \mathbf{Z}\otimes_{\mathbf{F}_{1}}\mathbf{Z} &\cong (\mathbf{Z}\setminus\{0\})^+\otimes_{\mathbf{F}_{1}}(\mathbf{Z}\setminus\{0\})^+\\ &\cong \left[\left(\Z\setminus\{0\}\right)\oplus\left(\Z\setminus\{0\}\right)\right]^+, \end{align*} where $X^+=X\sqcup\{0\}$. For $\mathbf{N}\otimes_{\mathbf{F}_{1}}\mathbf{N}$, writing $\mathbf{N}_*:=\mathbf{N}\setminus\{0\}$, we have a non-canonical isomorphism \begin{align*} \mathbf{N}\otimes_{\mathbf{F}_{1}}\mathbf{N} &\cong (\mathbf{N}_*\oplus\mathbf{N}_*)^+\\ &\cong \left((\mathbf{N},+,0)^{\oplus\mathbf{P}}\oplus(\mathbf{N},+,0)^{\oplus\mathbf{P}}\right)^+\\ &\overset{\text{non-canonically}}{\cong}((\mathbf{N},+,0)^{\oplus\mathbf{P}})^+\\ &\cong\left(\mathbf{N}_*\right)\sqcup\{0\}\\ &\cong\mathbf{N}, \end{align*} corresponding to a bijection $\mathbf{P}\times\mathbf{P}\cong\mathbf{P}$ of the square of the set of prime numbers with itself.

However, this argument fails for $\mathbf{Z}$, as we have $\mathbf{Z}\setminus\{0\}\cong(\mathbf{N},+,0)^{\oplus\mathbf{P}}\oplus\mathbf{Z}_2$, and thus there will be an extra factor of $\mathbf{Z}_{2}$ if we try to repeat the same argument, i.e.: $$\mathbf{Z}\otimes_{\mathbf{F}_{1}}\mathbf{Z}\cong((\mathbf{Z}\setminus\{0\})\oplus\mathbf{Z}_2)^+.$$

Therefore, while we have a non-canonical bijection \begin{align*} \mathrm{Spec}(\mathbf{Z}\otimes_{\mathbf{F}_{1}}\mathbf{Z})&\cong\mathrm{Spec}(\mathbf{Z}) \end{align*} of sets, the associated monoidal spaces aren't isomorphic, even non-canonically.