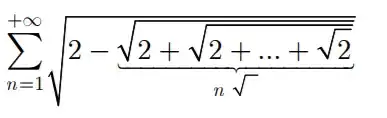Test the convergence of the series $\sum_{1}^{+\infty} \sqrt{2-\sqrt{2+\sqrt{2+...+\sqrt{2}}}}$

Question

I find some difficulty with the following exercise:

Test the convergence of the series $\sum_{1}^{+\infty} \sqrt{2-\sqrt{2+\sqrt{2+...+\sqrt{2}}}}$ (n square root) (*more clearly in the picture below)

I tested the limit of $a_n$ and it's $0$; I tried to calculate $\lim \frac{a_{n+1}}{a_n}$ but it seem to be difficult.

I don't know which theorem I should use to solve this problem. Can anyone help me or give me hint? Thank you so much.

Is that formula supposed to have exactly one minus sign in it? — RobertTheTutor, Aug 22 '21 at 15:55
@RobertTheTutor yes, if it's all plus (+) sign, limit of $a_n$ is not zero, so the series is diverge — Jaytone, Aug 22 '21 at 15:57

score 2 · Accepted Answer · answered Aug 22 '21 at 15:47

2

The main term of the series is $\sqrt{2-u_n}$, where $u_1=\sqrt{2}$ and $u_{n+1}=\sqrt{2+u_n}$. You can show by induction that $u_n=2\cos\left(\frac{\pi}{2^{n+1}}\right)$, therefore $$ \sqrt{2-u_n}=\sqrt{2-2\left(1-\frac{\pi^2}{2^{2n+3}}+o\left(\frac{1}{4^n}\right)\right)}=\frac{\pi}{2^{n+1}}\sqrt{1+o(1)}\sim\frac{\pi}{2^{n+1}} $$ Therefore $\sum\sqrt{2-u_n}$ converges.

answered Aug 22 '21 at 15:47

Tuvasbien

8,907

Thank you so much – Jaytone Aug 22 '21 at 15:48

Test the convergence of the series $\sum_{1}^{+\infty} \sqrt{2-\sqrt{2+\sqrt{2+...+\sqrt{2}}}}$

1 Answers1