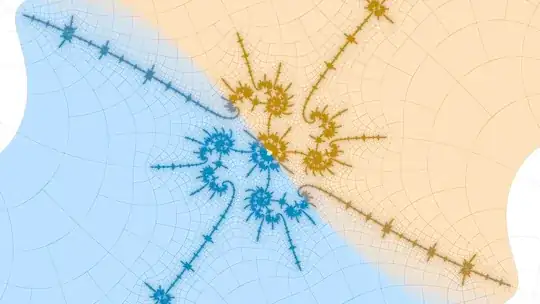
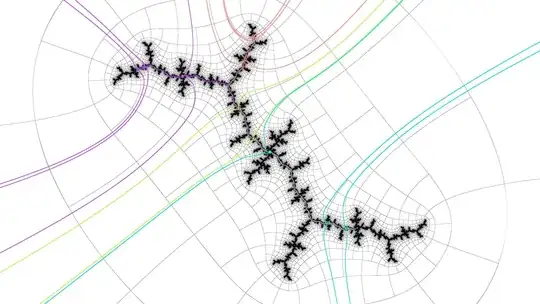
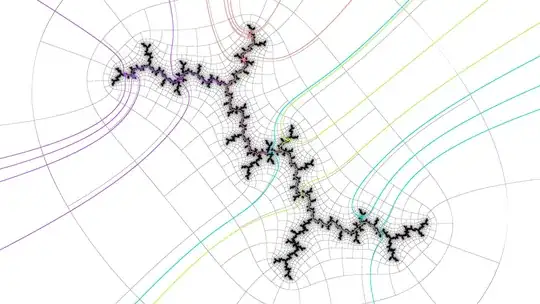
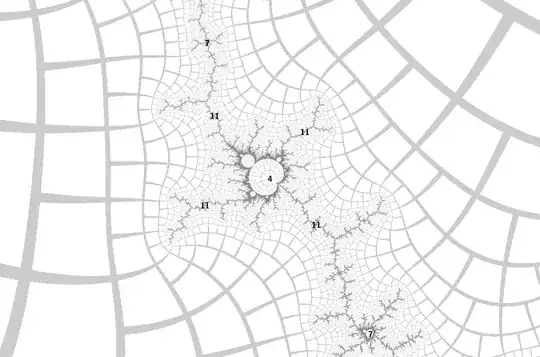
For example, how to tell efficiently which period $11$ island near a period $4$ island the coordinates $c \in \mathbb{C}$ correspond to, without tracing external rays? Ray tracing takes $O(N^2)$ time for dwell $N$; I need a more efficient algorithm as I want to do this for periods in the hundreds of thousands.
In this easy case, "front" can be distinguished from "back" because the two green marked points (corresponding to iterations $4$ and $8$, where iteration $1$ is $c$) in the Julia set are in the same direction vs opposite directions from the origin (one can use vector dot product to tell), but this is not always the case in the presence of spiraling filaments.
For "left" vs "right" I tried to see if certain points were clockwise or anticlockwise, but this also failed for a period 23 test case (it didn't spiral with the filaments).
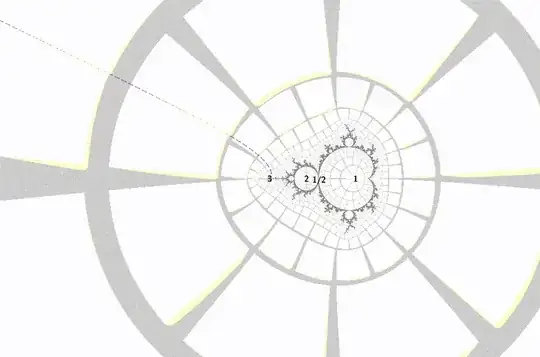
Four period 11 islands near north period 4 island, Mandelbrot set:
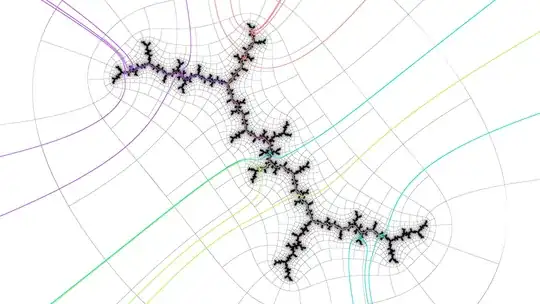
Julia set of center island p4:
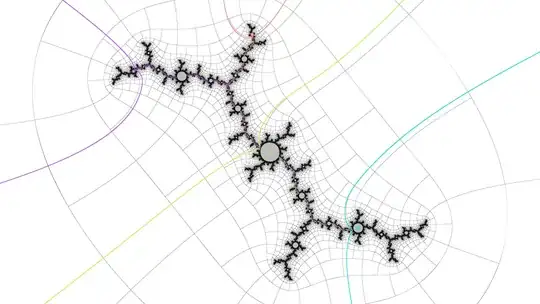
Julia set of front island p11:
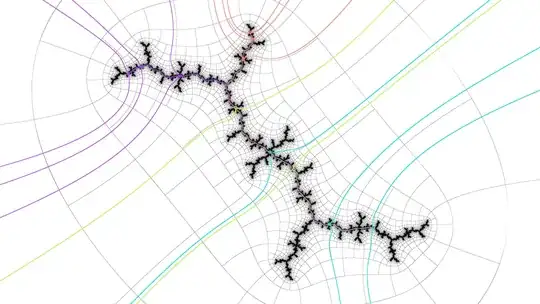
Julia set of back island p11:
Julia set of right island p11:
Julia set of left island p11:
Spiraling wakes (1/3 red + dotted, 2/3 blue x dashed) near a period 23 island in the Mandelbrot set:
Spiraling filaments near a period 23 island in the Mandelbrot set, coloured blue/orange for clockwise/anticlockwise nature of certain triples of points:
