2

Question:

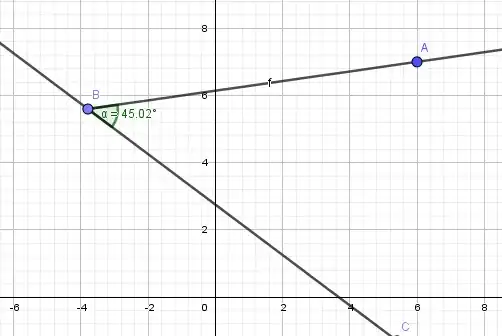
Find the equation of the straight line that passes through $(6,7)$ and makes an angle $45^{\circ}$ with the straight line $3x+4y=11$.

My solution (if you want, you can skip to the bottom):

Manipulating the given equation to get it to the slope-intercept form,

$$3x+4y=11...(i)$$

$$\implies 4y=-3x+11$$

$$\implies y=\frac{-3}{4}x+\frac{11}{4}$$

Let, the slope of (i) is $m_1=\frac{-3}{4}$, and the slope of our desired equation is $m_2$. Now, according to the question,

$$\tan(45^{\circ})=\pm\frac{-\frac{3}{4}-m_2}{1-\frac{3}{4}m_2}...(1)$$

$$\implies 1=\pm\frac{-\frac{3}{4}-m_2}{1-\frac{3}{4}m_2}$$

$$\implies \pm \frac{3}{4}+m_2=1-\frac{3}{4}m_2...(ii)$$

Picking positive value from (ii),

$$\frac{3}{4}+m_2=1-\frac{3}{4}m_2$$

$$\implies m_2(1+\frac{3}{4})=1-\frac{3}{4}$$

$$\implies m_2=\frac{1-\frac{3}{4}}{1+\frac{3}{4}}$$

$$\implies m_2=\frac{1}{7}$$

Picking negative value from (ii),

$$-\frac{3}{4}-m_2=1-\frac{3}{4}m_2$$

$$\implies -\frac{3}{4}-m_2=1-\frac{3}{4}m_2$$

$$\implies -m_2(1-\frac{3}{4})=1+\frac{3}{4}$$

$$\implies m_2=-\frac{1+\frac{3}{4}}{1-\frac{3}{4}}$$

$$\implies m_2=-7$$

Picking $m_2=\frac{1}{7}$, the equation of the straight line that passes through $(6,7)$,

$$\frac{y-7}{x-6}=\frac{1}{7}$$

$$\implies 7y-49=x-6$$

$$\implies -x+7y-43=0$$

$$\implies x-7y+43=0...(iii)$$

Picking $m_2=-7$, the equation of the straight line that passes through $(6,7)$,

$$\frac{y-7}{x-6}=-7$$

$$\implies -7x+42=y-7$$

$$\implies 7x+y-49=0...(iv)$$

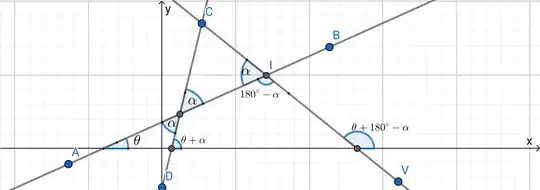
The general form of equation (1) is,

$$\tan\theta=\pm \frac{m_1-m_2}{1+m_1m_2}$$

Here, $\pm$ has been included to include both the acute and the obtuse angles that are formed when two lines with slopes $m_1$ and $m_2$ intersect each other.

Now, I used this equation to find the straight line that makes $45^{\circ}$ with (i). Why am I getting 2 values of $m_2$ when there is only one value of $m_2$ in the general form of the equation? How can I reconcile between my getting of 2 values of $m_2$ with the $\pm$ sign arising due to the acute and obtuse angles?

tryingtobeastoic
  • 3,176
  • 4
    I don't understand what you're asking for. You have the original line, and have found two lines at 45 degrees from that original line. What is puzzling about that? – Jaap Scherphuis Sep 07 '21 at 15:55
  • Two different lines can be inclined at the same angle with a given line like $y=x$ and $y=-x$ both are inclined at $45°$ with $x-$ axis, where the inclination is measured in anticlockwise and clockwise direction respectively with the positive direction of $x-$ axis. I don't understand what intuition do you need for this. – Aman Kushwaha Sep 07 '21 at 16:02
  • @JaapScherphuis I don't understand the intuition behind getting 2 values of $m_2$. In the derivation of (1), $m_1$ and $m_2$ are fixed, so why are we getting 2 values of $m_2$ here? – tryingtobeastoic Sep 07 '21 at 16:09
  • @AmanKushwaha I don't understand the intuition behind getting 2 values of m2. In the derivation of (1), m1 and m2 are fixed, so why are we getting 2 values of m2 here? – tryingtobeastoic Sep 07 '21 at 16:10
  • @AbuSafwanMdFarhan we never "fixed" $m_2$ while solving. The slope of the required line was variable initially and that's what you obtained. Maybe you did not pay heed to the fact that two such lines exist and straightaway started with the algebra. – RiverX15 Sep 07 '21 at 16:21
  • A line passing through $(6,7)$ with varying slope is plotted here: https://www.desmos.com/calculator/8navr7tye2 .You can use the slider to rotate this line. What you did in your algebraic calculation is that you were trying to find which of these infinitely many lines (passing through $(6,-7)$) make an angle of $45°$ with the given line. And you got two such lines. Any problem till here? – Aman Kushwaha Sep 07 '21 at 16:27
  • @RyanG I edited it. – tryingtobeastoic Sep 07 '21 at 17:08
  • 1
    @RyanG Thanks for your support. I've written an answer and it's somewhat analogous to your comments. If you want to suggest any edit, I would accept that. Thank you. – Aman Kushwaha Sep 07 '21 at 20:22
  • The slope angle of a straight line is indeterminate to 180°, hence you could find four solutions, which are in fact pairwise identical. –  Sep 08 '21 at 06:05

3 Answers3

2

I think your problem is regarding this equation:

$$\tan(45^{\circ})=\pm\frac{-\frac{3}{4}-m_2}{1-\frac{3}{4}m_2} \tag{1} \label{1}$$ (You are using equation tags (i) and (1) both creating confusion among the readers)

Your misconception: You think the two values of $\theta$ one can get by solving $\tan{\theta}= |\frac{m_1-m_2}{1+m_1m_2}|$ represent acute angle and the obtuse angle respectively between the lines with slopes $m_1$ and $m_2$.

Fact: In the above formula $\theta$ is always the acute angle between the lines with slopes $m_1$ and $m_2$. $\theta$ is simply equal to $|\tan^{-1}{m_1}-\tan^{-1}{m_2}|$ from which one derives the above formula.(In your question, of course $\theta=45°$ is acute and for that acute angle only, you are getting two values of $m_2$)

Further information: The equation of lines passing through point $(x_1,y_1)$ making an angle $\alpha$ with the line $y=mx+c$ are given by:

$y-y_1=\tan(\theta-\alpha)(x-x_1)$ and $y-y_1= \tan(\theta-\alpha)(x-x_1)$, where $\tan{\theta}=m$

enter image description here

Here the two lines $CD$ and $CV$ passing through $C(x_1,y_1)$ make an angle $\alpha$ with line $AB$ having slope $\tan{\theta}$. You'll always get exactly two such lines and their slopes will always be $\tan{(\theta+\alpha)}$ and $\tan{(\theta+180°-\alpha)}=\tan{(\theta-\alpha)}$. These are the two slopes you get while solving for $m_2$ in $(\ref{1})$. Notice that the angles $\theta + \alpha$ and $\theta - \alpha$ are not acute obtuse pair.

Note: Acute and obtuse have nothing to do here unless you were given an inclination angle which is obtuse, for which you simply have to find the corresponding acute angle between the lines and use that for $\theta$ in $\tan{\theta}= |\frac{m_1-m_2}{1+m_1m_2}|$ or alternatively, you can use this formula: $\tan{\theta_{obtuse}}= - |\frac{m_1-m_2}{1+m_1m_2}|$ where $\theta_{obtuse}$ is the obtuse angle between the lines with slopes $m_1$ and $m_2$.

Answering some questions after reading your edit:

Here, $\pm$ has been included to include both the acute and the obtuse angles that are formed when two lines with slopes $m_1$ and $m_2$ intersect each other.

No. You are completely wrong there. $\pm$ is there because the angle $\theta$ can be measured from two different directions namely clockwise and anticlockwise.This fact is responsible for two different lines satisfying one condition of inclination angle. See the figure attached in my answer.

Why am I getting 2 values of $m_2$ when there is only one value of $m_2$ in the general form of the equation?

You might be thinking $(\ref{1})$ is one equation, but that equation is actually a simpler way of writing two equations connected with "or". This is pretty obvious. Why can't you expect two different solutions of two different equations?

Aman Kushwaha
  • 1,664
  • @AbuSafwanMdFarhan Forgive me if I misunderstood your query. I tried to include all the information I thought that might prove helpful. Let me know if you have any problem in understanding any part or – Aman Kushwaha Sep 07 '21 at 18:33
  • Thanks for your response! Can't the acute angle measured in the clockwise direction also represent the obtuse angle formed between any two straight lines in (1)? Also, could you please source me to a ta good derivation for (1)? A link or the name of a textbook will do. I think my book does a terrible job at it. – tryingtobeastoic Sep 08 '21 at 04:31
  • Contrary to your answer, all the derivations say that in (1), acute and obtuse angles are being measured. This for example https://www.math-only-math.com/angle-between-two-straight-lines.html. Could you please clarify this for me? – tryingtobeastoic Sep 08 '21 at 04:51
  • I posted another question here: https://math.stackexchange.com/q/4244744/768162. You can have a look at it if you want. – tryingtobeastoic Sep 08 '21 at 05:04
  • In your question, equation (1) already had $\theta=45°$ fixed, which is acute, $\tan{45°}$ is positive. I was talking about that equation in my whole answer. The intuition behind presence of $\pm$ in (1) is what I said about direction. How does the question about acute-obtuse arise when $\theta$ is already given.The RHS in (1) must be positive and would be equal to $+1$ for two values of $m_2$ "picking $+$ or $-$ signs from $(ii)$". After picking either of the signs in (1), you get $m_2$ such that RHS in (1) automatically becomes positive, obviously because $\theta$ is already acute. – Aman Kushwaha Sep 08 '21 at 06:10
  • For example, when you picked the negative sign, you got $m_2=-7$. This $m_2$ made $\frac{m_1-m_2}{1+m_1m_2}$ negative and hence $- \frac{m_1-m_2}{1+m_1m_2}$ which is the RHS became positive (and equal to $+1$). At last, this is very apparent but I think now I have to say this: $45°$ is $45°$. This is an acute angle. How can this represent obtuse angle between any two lines! @AbuSafwanMdFarhan – Aman Kushwaha Sep 08 '21 at 06:17
  • Regarding the other question you asked, that has $θ$ as variable not constant, the negative one of $+\frac{m_1−m_2}{1+m_1m_2}$ or $-\frac{m_1−m_2}{1+m_1m_2}$ obviously implies $θ$ is either obtuse or belong to $\left({-\pi \over 2},0\right)$ depending upon how you define $θ$. – Aman Kushwaha Sep 08 '21 at 06:35
  • @AmanKushwaha I have put you through a lot of pain, and I finally understood what you had been talking about this morning. I thank you from the bottom of my heart. If I have made any mistakes, please forgive me. – tryingtobeastoic Sep 09 '21 at 16:05
  • +1. For reference, my original comments have been moved into this sequel. – ryang Sep 18 '21 at 04:35
0

You have a right triangle with the right angle at (6, 7) and the line 3x+ 4y= 11 as hypotenuse. The "two lines" are the two legs of the triangle.

user247327
  • 18,710
0

We have to be mindful about sign of slope

To the given inclination $ \tan^{-1} (-3/4) = - 36. 87 ^{\circ}$ add, resulting in $ 45 ^{\circ}- 36.87 ^{\circ} = 8.13^{\circ}$ positive ( counter clockwise) to x-axis and you have only one straight line solution AB. Other solution is spurious, needs to be discarded.

enter image description here

Narasimham
  • 40,495