Bottom to top explanation of the Mahanalobis distance?

Question

I'm studying Pattern recognition and statistics and almost every book I open on the subject I bump into the concept of Mahanalobis distance. The books give sort of intuitive explanations, but still not good enough ones for me to actually really understand what is going on. If someone would ask me "What is the Mahanalobis distance?" I could only answer: "It's this nice thing, which measures distance of some kind" :)

The definitions usually also contain eigenvectors and eigenvalues, which I have little trouble connecting to the Mahanalobis distance. I understand the definition of eigenvectors and eigenvalues, but how are they related to the Mahanalobis distance? Does it have something to do with changing the base in Linear Algebra etc.?

I have also read these former questions on the subject:

https://stats.stackexchange.com/questions/41222/what-is-mahanalobis-distance-how-is-it-used-in-pattern-recognition

Intuitive explanations for Gaussian distribution function and mahalanobis distance

http://www.jennessent.com/arcview/mahalanobis_description.htm

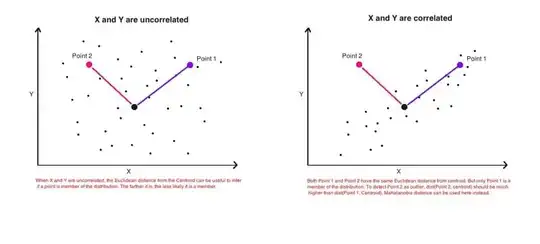
The answers are good and pictures nice, but still I don't really get it...I have an idea but it's still in the dark. Can someone give a "How would you explain it to your grandma"-explanation so that I could finally wrap this up and never again wonder what the heck is a Mahanalobis distance? :) Where does it come from, what, why?

I will post this question on two different forums so that more people could have a chance answering it and I think many other people might be interested besides me :)

Thank you in advance for help!

Answer 1

As a starting point, I would see the Mahalonobis distance as a suitable deformation of the usual Euclidean distance $d(x,y)=\sqrt{\langle x,y \rangle}$ between vectors $x$ and $y$ in $\mathbb R^{n}$. The extra piece of information here is that $x$ and $y$ are actually random vectors, i.e. 2 different realizations of a vector $X$ of random variables, lying in the background of our discussion. The question that the Mahalonobis tries to address is the following:

"how can I measure the "dissimilarity" between $x$ and $y$, knowing that they are realization of the same multivariate random variable?"

Clearly the dissimilarity of any realization $x$ with itself should be equal to 0; moreover, the dissimilarity should be a symmetric function of the realizations and should reflect the existence of a random process in the background. This last aspect is taken into consideration by introducing the covariance matrix $C$ of the multivariate random variable.

Collecting the above ideas we arrive quite naturally at

$$D(x,y)=\sqrt{\langle (x-y),C^{-1}(x-y)\rangle} $$

If the components $X_i$ of the multivariate random variable $X=(X_1,\dots,X_n)$ are uncorrelated, with, for example $C_{ij}=\delta_{ij}$ (we "normalized" the $X_i$'s in order to have $Var(X_i)=1$), then the Mahalonobis distance $D(x,y)$ is the Euclidean distance between $x$ and $y$. In presence non trivial correlations, the (estimated) correlation matrix $C(x,y)$ "deforms" the Euclidean distance.

Answer 2

I found this link useful for understanding what Mahalanobis distance measures actually. The following image captures the essence very well:

If your dataset has a strong correlation as in the plot on the right, you probably want Point 2 to be more distant to black point in the center than the Point 1, although they have the same Euclidean distance. As Avitus pointed out, multiplying with the inverse of the correlation matrix deforms the Eucledean distance so that Point 2 becomes more distant than Point 1.