Question:
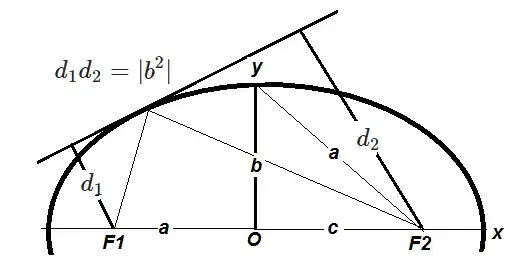
Show that the product of the lengths of the perpendiculars drawn from the points $(\pm c,0)$ to the straight line $bx\cos\theta+ay\sin\theta-ab=0$ is $b^2$ when $a^2=b^2+c^2$.
My attempt:
Let, the length of the perpendicular on drawn upon $bx\cos\theta+ay\sin\theta-ab=0$ from $(c,0)$ is $d_1$ and the length of that drawn upon the same from $(-c,0)$ is $d_2$. Now,
$$d_1=\frac{|bc\cos\theta+0-ab|}{\sqrt{b^2\cos^2\theta+a^2\sin^2\theta}}$$
$$\implies d_1=\frac{|bc\cos\theta-ab|}{\sqrt{b^2\cos^2\theta+a^2\sin^2\theta}}$$
Again,
$$d_2=\frac{|-bc\cos\theta-ab|}{\sqrt{b^2\cos^2\theta+a^2\sin^2\theta}}$$
Now,
$$d_1d_2=\frac{|-(bc\cos\theta-ab)(bc\cos\theta+ab)|}{{b^2\cos^2\theta+a^2\sin^2\theta}}$$
$$\implies d_1d_2=\frac{|a^2b^2-b^2c^2\cos^2\theta|}{{b^2\cos^2\theta+a^2\sin^2\theta}}$$
$$\implies d_1d_2=\frac{|a^2b^2-b^2c^2\cos^2\theta|}{{b^2\cos^2\theta+a^2(1-\cos^2\theta)}}$$
$$\implies d_1d_2=\frac{|a^2b^2-b^2c^2\cos^2\theta|}{{b^2\cos^2\theta+a^2-a^2\cos^2\theta}}$$
$$\implies d_1d_2=\frac{|a^2b^2-b^2c^2\cos^2\theta|}{a^2-(a^2-b^2)\cos^2\theta}$$
$$\implies d_1d_2=|\frac{b^2(a^2-c^2\cos^2\theta)}{a^2-(a^2-b^2)\cos^2\theta}|$$ [$a^2-(a^2-b^2)\cos^2\theta$ is positive, so bringing it inside the modulus sign doesn't make a difference]
$$\implies d_1d_2=|\frac{b^2(a^2-(a^2-b^2)\cos^2\theta)}{(a^2-(a^2-b^2)\cos^2\theta)}|$$ [Given, $a^2=b^2+c^2\implies c^2=a^2-b^2$]
$$d_1d_2=|b^2|$$(shown?)
The question asked me to show that $d_1d_2=b^2$, but I showed them that $d_1d_2=|b^2|$. So, is there something wrong with my process, or is there something wrong with the question?