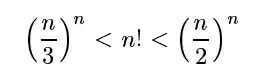Proof by induction using definition of e

Asked Sep 24 '21 at 11:15

Active Sep 24 '21 at 11:15

Viewed 50 times

I'm working with this example that I'm trying to prove using induction:

I have two inequalities, so I have to do 2 induction proofs for each inequality seperately.

Treating the left inequality, after the base case and the induction assumption, I reach this point:

$(m+1)! > (m+1)(\frac{m}{3})^m$

Now, the question arises, is $(m+1)(\frac{m}{3})^m>(\frac{m+1}{3})^{m+1}$

I think that you can then see, after some simplications, that we get:

$3 > (1+1/m)^m$

Which then can be proved using the definition of e, I assume? Either way, I'd like to hear about your opinions, is this a good way of solving the problem using induction?

Thanks!

asked Sep 24 '21 at 11:15

Tanamas

1,837

8

Does this answer your question? Factorial Inequality problem $\left(\frac n2\right)^n > n! > \left(\frac n3\right)^n$ – José Carlos Santos Sep 24 '21 at 11:18
1

If you also show that $(1+\frac{1}{m})^m$ is strictly increasing , then this approach is fine. – Peter Sep 24 '21 at 11:28
1

$(1+1/m)^m < 3$ ⇔ $1+t < 3^t$, which is much easier to prove. – Ivan Kaznacheyeu Sep 24 '21 at 12:33
@Peter How would one show that it's strictly increasing, without using derivatives? Could I just compare the ratio of the (m+1):th term and m:th term? – Tanamas Sep 24 '21 at 12:42
@JoséCarlosSantos Thank you :) – Tanamas Sep 24 '21 at 12:42
@JoséCarlosSantos: Here OP asks for proof using induction, whereas the question you linked asks for proof not using induction – J. W. Tanner Sep 26 '21 at 17:03
1

@J.W.Tanner Right. I've rectracted my vote. – José Carlos Santos Sep 26 '21 at 17:07

Proof by induction using definition of e

0 Answers0