Integral $\int_0^\infty \frac{x \ln(1+x^2)}{e^{2 \pi x}+1}\,dx=\frac{19}{24}-\frac{23}{24}\ln 2-\frac{\ln A}{2}$

Question

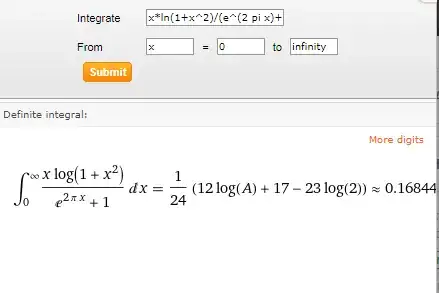
Edit: A friend of mine used a contour integral to solve this problem and his final answer matches with mine. It seems that Wolphram´s is incorrect

---

I saw the following integral here and went to proof it.

$$\int_0^\infty \frac{x \ln(1+x^2)}{e^{2 \pi x}+1}\,dx=\frac{19}{24}-\frac{23}{24}\ln 2-\frac{\ln A}{2}$$

I started using the following identity

$$\frac{1}{e^{2\pi x}+1}=\frac{1}{e^{2\pi x}-1}-\frac{2}{e^{4\pi x}-1} \tag{1}$$

To rewrite the integral as following

$$\int_0^\infty \frac{x \ln(1+x^2)}{e^{2 \pi x}+1}\,dx=\int_0^\infty\frac{x \ln(z^2+x^2)}{e^{2 \pi x}-1}\,dx-2\int_0^\infty\frac{x \ln(z^2+x^2)}{e^{4\pi x}-1}\,dx \tag{2}$$

In my previous post I established the value of the first integral of the R.H.S. of $(2)$

$$\int_{0}^{\infty} \frac{x \ln \left(1+x^{2}\right)}{e^{2 \pi x}-1} d x=\zeta^{\prime}(-1)+\frac12\ln 2 +\frac12 \ln \pi-\frac{3}{4} \tag{3}$$

So it remains to evaluate

$$\int_0^\infty\frac{x \ln(1+x^2)}{e^{4\pi x}-1}\,dx$$

To this end, I followed the same procedure I used in the previous post. Consider the integral

$$J(z)=\int_0^\infty\frac{x \ln(z^2+x^2)}{e^{4\pi x}-1}\,dx \tag{4}$$

And differentiate it w.r. to $z$ to get

$$J^{\prime}(z)=\int_0^\infty\frac{2zx }{(z^2+x^2)(e^{4\pi x}-1)}\,dx \tag{5}$$

Then comparing it with Binet´s formula

$$\int_0^\infty\frac{x }{(z^2+x^2)(e^{2\pi x}-1)}\,dx=\frac{\log(z)}{2}-\frac{\psi(z)}{2}-\frac{1}{4z} \tag{6}$$

And after a change in parameter and a change of variable we find that

$$\int_0^\infty\frac{2sx }{(s^2+x^2)(e^{4\pi x}-1)}\,dx=s \ln(2s)-s\psi(2s)-\frac{1}{4} \tag{7}$$

Now, integrate $(7)$ with respect to $s$ from $0$ to $z$ and then let $z \to 1$, I got

$$\int_0^\infty\frac{x \ln(1+x^2)}{e^{4\pi x}-1}\,dx=\frac{\ln \pi}{4}-\frac{36}{48}+\frac{35}{48} \ln2+\frac14 \zeta^{\prime}(-1) \tag{7}$$

Since I could not find the answer of this integral nowhere, I went to Wolfram Alpha to see whether it matches with it´s solution, but it doesn´t! Nevertheless, I sticked to it, and together with $(3)$ I plugged it´s values in $(2)$.

To get the final answer

$$\begin{aligned} \int_0^\infty \frac{x \ln(1+x^2)}{e^{2 \pi x}+1}\,dx&=\zeta^{\prime}(-1)+\frac12\ln 2 +\frac12 \ln \pi-\frac{3}{4}-2\left(\frac{\ln \pi}{4}-\frac{36}{48}+\frac{35}{48}\ln2+\frac14 \zeta^{\prime}(-1) \right)\\ &=\frac12\zeta^{\prime}(-1)-\frac{23}{24}\ln 2+\frac{18}{24}\\ &=\frac12\left(\frac{1}{12}-\ln A \right)-\frac{23}{24}\ln 2+\frac{18}{24}\\ &=\frac{19}{24}-\frac{23}{24}\ln 2-\frac{\ln A}{2} \qquad \blacksquare \end{aligned} $$

Now, this answer matches with the answer from where I saw the integral, but it does not match Wolfram Alpha´s answer.

The obvious question is: Which one is correct??

Answer 1

It can be shown by the Abel-Plana formula, hoping for convergence, that:

$$\sum_{x\ge0} f(x)=\frac{f(0)}2 +\int_0^\infty f(x)dx+i\int_0^\infty\frac{f(ix)-f(-ix)}{e^{2\pi x}-1}dx$$

Note that when $f(x)=-\frac i2 x \ln(1-x^2)\implies f(ix)-f(-ix)=x\ln(x^2+1)$:

Let’s plug in to the formula:

$$\sum_{x\ge0} -\frac i2 x \ln(1-x^2) =\frac{-\frac i2 0 \ln(1-0^2)}2 +\int_0^\infty -\frac i2 x \ln(1-x^2) dx+i\int_0^\infty\frac{-\frac i2 x \ln(1-x^2)- -\frac i2 x \ln(1-x^2)}{e^{2\pi x}-1}dx\implies \sum_{x\ge0} -\frac i2 x \ln(1-x^2) -0- \int_0^\infty -\frac i2 x \ln(1-x^2) dx =i\int_0^\infty\frac{x\ln(x^2+1)}{e^{2\pi x}-1}dx$$

Let’s collect our results:

$$-i\sum_{x\ge0} -\frac i2 x \ln(1-x^2) - -i\int_0^\infty -\frac i2 x \ln(1-x^2) dx =\int_0^\infty\frac{x\ln(x^2+1)}{e^{2\pi x}-1}dx= \frac12\int_0^\infty x \ln(1-x^2) dx -\frac12 \sum_{x\ge0} x \ln(1-x^2) $$

This was an attempt using the formula. There should be a better method to use. Please correct me and give me feedback!