1

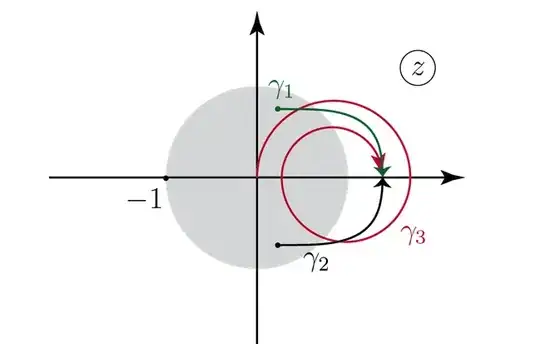
Consider we have a function that is defined in a unit disk in complex plane. Let it be $$F_\alpha(z)=\displaystyle\int\limits_{0}^{1} (1-zt)t^\alpha dt,\alpha>0$$
I have to evaluate $F_\alpha (x_1)-F_\alpha (x_2)$. Where $x_1$ and $x_2$ are depends on the $\gamma_1$ and $\gamma_2$

$\color{black}{\text{ways of possible analytical continuation}}$: enter image description here

The problem says that $\gamma_i$ is a possible way of analytical continuation of $F_\alpha (z)$. I just can't understand what I should do to solve it.
P.S. Function in my original problem is different ( $F_\alpha (z)=\displaystyle\int\limits_0^1\displaystyle\frac{t^\alpha(1-t)^\alpha}{1-zt}dt$ ), but i just want to find out how to solve this type of problems
Sorry for my English

mark
  • 754
Nogaromo
  • 9
  • 1
    If you evaluate the integral, you'll see that your first $F_\alpha(z)$ doesn't have branch points. For the second function, prove that $G_\alpha(z) = \int_0^1 t^\alpha (1 - t)^\alpha/(1 - z t) , dt$ is analytic on $\mathbb C \setminus [1, \infty)$. It follows that $F_\alpha(x_1) - F_\alpha(x_2) = G_\alpha(x + i0) - G_\alpha(x - i0)$. Then prove that the limits can be written in this way. – Maxim Oct 18 '21 at 13:58

0 Answers0