Examine the following function for relative extrema and saddle points: $$f(x, y) = 9x^2-5y^2-54x-40y+4.$$ I did this and got that the point should be at $(3, -4, 3)$. Is that right? Also, how do I know if it is a saddle point or a minimum?
2 Answers
Hints:
- Your solution is correct, the critical point is $(3, -4)$ and the function value $f(x,y) = 3$ at the critical point.
- There are no global min or max
- There are no local min or max
- To determine if it is saddle, you look at the determinant of the Hessian, $$\det(H) = -180 < 0 \rightarrow \text{saddle}$$
So we have a saddle at the critical point.
See my response here for details: Maximum and minimum absolute of a function $(x,y)$
Graphically, we can see this:
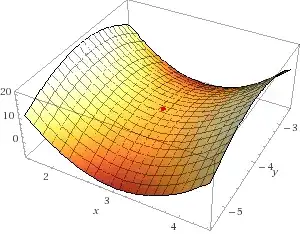
-
Yes indeed, you're having a great day! $\oplus $ – amWhy Jun 24 '13 at 02:32
The point should be $(3,-4)$. Now recall the following useful fact. Suppose that $f_x(a,b)=0$ and $f_y(a,b)=0$. Let $$D(x,y)=f_{xx}f_{yy} -(f_{xy})^2.$$
If $D(a,b)\lt 0$, we have a saddle point at $(a,b)$.
When you calculate, you will find that is the case here.
But for completeness, we add some information.
If $D(a,b)\gt 0$ and $f_{xx}(a,b)\lt 0$, we have a local maximum at $(a,b)$.
If $D(a,b)\gt 0$ and $f_{xx}(a,b)\gt 0$, we have a local minimum at $(a,b)$.
If $D(a,b)=0$ we do not learn whether we have a local max, a local min, or a saddle point at $(a,b)$. The test is inconclusive.
Remark: We have used the notation $f_{x}$ where your course might use $\frac{\partial f}{\partial x}$, and $f_{xx}$ where your course might use $\frac{\partial^2 f}{\partial x^2}$, with the rest of the notations we hope self-explanatory. Your course may use the term Hessian.
- 507,029