Geometric proof for harmonic form?

Asked Oct 22 '21 at 21:30

Active Oct 23 '21 at 04:19

Viewed 169 times

I am a Maths teacher, and I'd like to teach my students the harmonic identities:

$$R\sin(x + y) = A\sin(x) + B\cos(y)$$

and

$$R\cos(x + y) = A\sin(x) - B\cos(y)$$

I don't want to do it the algebraic way, as a few years ago I saw a really exciting lesson which proved it geometrically. The basis of the proof was the following problem:

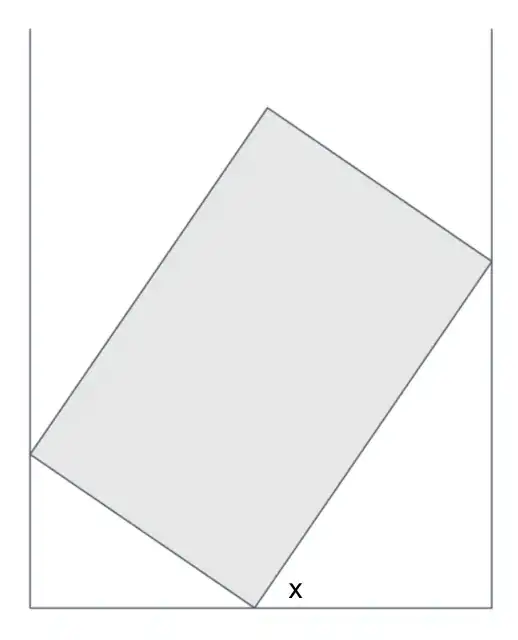
Someone is trying to park a car. The car’s dimensions are $3\,\mathrm{m} \times 1\,\mathrm{m}$. The bay is $4\,\mathrm{m} \times 2\,\mathrm{m}$. What is the worst angle ($x$ in the diagram) the car could be parked, but still be in the space?

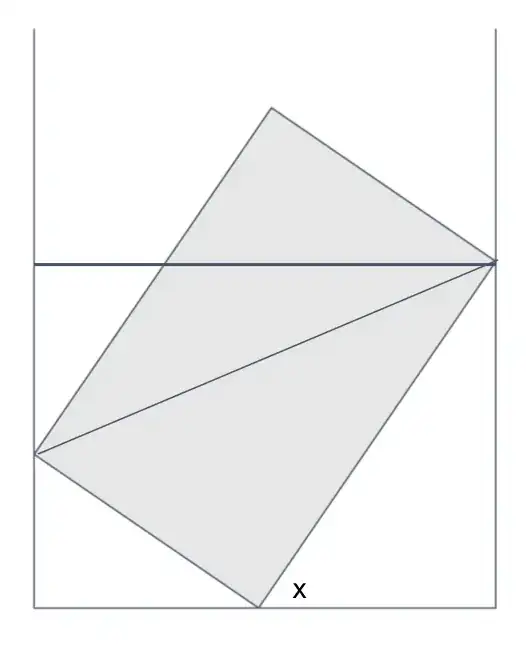
If you draw in the following two lines, where one of them is just parallel to the base of the parking space, and the other is the diagonal of the car's dimensions (which can be found using Pythagoras) you can arrive at the identities.

The problem is, this is super chunky and I'm wondering if there is a neater geometric proof out there?

edited Oct 23 '21 at 04:19

user10354138

33,239

asked Oct 22 '21 at 21:30

harpomiel

This answer shows a version I did, but it's pretty-much the same as yours. That answer doesn't show the difference identity, but that appears in the linked figure on my trigonography site. – Blue Oct 22 '21 at 21:48
I see x. Where is y? – Moti Oct 23 '21 at 20:07
I can derive a geometric structure that depicts the identities but I did not prove it. – Moti Oct 24 '21 at 01:56

Geometric proof for harmonic form?

0 Answers0