For $$ I=\int_{1}^{\infty}\int_{x}^{\infty}f(x,y)\text{d}y\text{d}x $$, let $u=x+y,v=y$, I found $$ I=\frac{1}{2}\int_{1}^{\infty}\int_{v+1}^{\infty}f(u-v,v)\text{d}u\text{d}v. $$ But in here, also changes $u=x+y,v=y$ but gives different results. I really don't understand where are they from? Thanks for your time!
Asked
Active
Viewed 54 times
1 Answers
1
This is the region in the $xy$-plane you are integrating over: $y \ge x \ge 1$
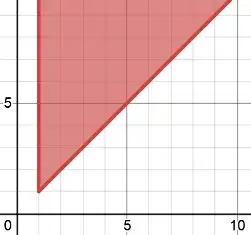
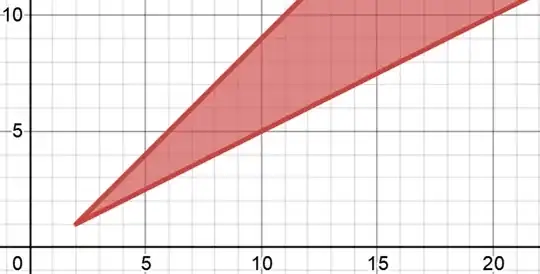
In terms of $u$ and $v$, this becomes $v \ge u - v \ge 1$, or $2v \ge u \ge 1 + v$.
The Jacobian of the change of variables is $$\left|\begin{array}{cc}\frac{\partial u}{\partial x}&\frac{\partial v}{\partial x}\\\frac{\partial u}{\partial y}&\frac{\partial v}{\partial y}\end{array}\right|= \left|\begin{array}{cc}1&0\\1&1\end{array}\right| = 1$$
So your change of variables should be $$I = \int_1^\infty\int_{v+1}^{2v} f(u - v,v)\,du\,dv$$ with neither the factor of $\frac 12$ nor $u$ going unfettered to $\infty$.
In the other thread, the order of integration is also reversed. The lowest value of $v$ is $1$, so the lowest value of $u$ is $2$. And of course $u$ can be arbitrarily large. So when $u$ is the primary variable, its limits are $2$ to $\infty$. From $2v \ge u$, we get $v \ge \frac u2$. From $u \ge 1 + v$ we get $v \le u - 1$. Thus reversing the order of integration yields $$I = \int_2^\infty\int_{u/2}^{u - 1}f(u - v,v)\,dv\,du$$ matching their limits of integration.
Paul Sinclair
- 43,643