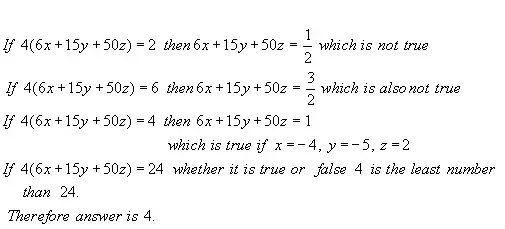I am stuck on the following problem:
The smallest positive integer in the set $\{24u+60v+200w : u,v,w \in \Bbb Z\}$is given by which of the following number?
The options are: $2,4,6,24$.
Since $24u+60v+200w=4(6u+15v+50w)$, I think the answer is between 4 and 24. Can someone explain it?
HINT: It shouldn't be too hard to convince yourself (or even prove) that the greatest common divisor of 24, 60 and 200 must also divide $24u+60v+200w$ for any $u,v,w\in \mathbb{Z}$ and in fact we can find $u,v$ and $w$ for any multiple of the gcd.
Hint: The greatest common divisor of $6$ and $15$ is $3,$ so we can get any integer multiple of $3$ from $6u+15v$ by choosing appropriate $u,v$. Now put $w=2,$ and choose an appropriate integer multiple of $3$ for $6u+15v$ to be.
More generally, given integers $n_1,n_2,...,n_k,$ the least positive integer in the set of sums $n_1m_1+n_2m_2+...+n_km_k$ (with the $m_j\in\Bbb Z$) will be the greatest common divisor of $n_1,n_2,...,n_k$.
