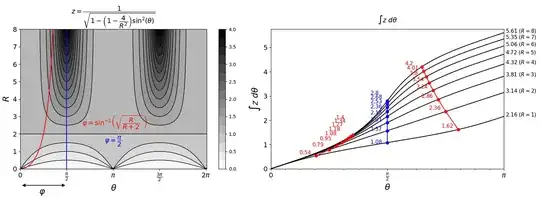
I explored the convolution of $\arcsin$ distributions SE. Here I found the following identity empirical (allot of trial, error and luck):
typo: $1-\frac{1}{R^2}$ should be $1-\frac{\color{red}{4}}{R^2}$. As pointed out by first answer.
$$F\left(\sin^{-1}\left(\sqrt{\frac{R}{R+2}}\right) \biggr\rvert 1-\frac{\color{red}{4}}{R^2}\right) \stackrel{?}{=}\frac{1}{2}\cdot K\left(1-\frac{\color{red}{4}}{R^2}\right) \tag{1}$$
With $F$ the incomplete and $K$ the complete elliptic integral and: $-2 \leq R \leq 2$. I only have numerical confirmation with WA online and Python (see: SE).
Looking at definitions: $$F(\varphi \rvert k^2)=\int_{0}^{\varphi} \frac{ \ d \theta}{\sqrt{1-k^2 \sin^2(\theta)}}$$ $$K(k)=\int_{0}^{\frac{\pi}{2}}\frac{ \ d \theta}{\sqrt{1-k^2 \sin^2(\theta)}} $$
If the identity $(1)$ is correct how to interpret: $$\sin^{-1}\left(\sqrt{\frac{R}{R+2}}\right) \neq \frac{\pi}{2}$$
Seems maybe related to: SE, this article is currently outside my math level.
Seeking a proof (comments: hints/tips to continue studying). Do not know where to start. Note that I am novice with elliptic integrals.