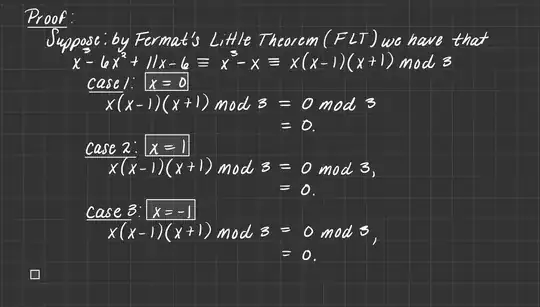Show that $x^3 - 6x^2 + 11x - 6$ is divisible by $3, \forall x \in \mathbb{Z}$.

Question

Update: I feel as though I'm doing something very wrong here.

Thank you all for the great suggestions! I am going to take the suggestions and try to shorten my proof. Again, I appreciate you all!

Hello, again. I hope that uploading an image of my proof is acceptable. Typing the proof out would be painful, but if typing the proof out is necessary to receive help, then I will do so.

I have tried this proof using several methods: direct, contradiction and induction. Direct proof by using the additive group of $\mathbb{Z_3}$ was the only thing that seemed to work. However, when I choose an integer outside of the group, I still find that I have the same result. I do not know if that is ok. I do not know if this proof is wholly flawed or not. Thank you all for your help and patience.

@Nightflight I mean that I chose the numbers 3, 4, and 5 and I got the same result. — India J. Delta, Nov 05 '21 at 21:46
The group $\mathbb{Z}_3$ is not a subset of $\mathbb{Z}$; it is a set of equivalent classes. It is not quite right to say "integer outside the group $\mathbb{Z}_3$". — , Nov 05 '21 at 21:52
Alt. hint: $,x^3 \color{red}{-x+x} - 6x^2 + 11x - 6=x^3-x - 6(x^2-2x+1)=x(x-1)(x+1)+3n,$. — dxiv, Nov 05 '21 at 21:53
Thank you @LouisPan. What is the correct way to say what I was intending? — India J. Delta, Nov 05 '21 at 21:55
Note that $x^3-6x^2+11x+6\equiv x(x^2+11)\equiv x(x^2+2),(mod,3)$. Then, take $x=3n, 3n+1$ or $3n+2$ — minmax, Nov 05 '21 at 21:57
Does this answer your question? Using induction prove $n^3-n$ is divisible by 3 whenever n is a positive number. — Bill Dubuque, Nov 22 '21 at 00:30
Your $,f(x) = x^3-x + 3(-2x^2+4x-2),$ so it suffices to show $,3\mid x^3-x,$ which has been done here hundreds of times, e.g. see the linked dupe and its links. — Bill Dubuque, Nov 22 '21 at 00:31

score 5 · Answer 1 · answered Nov 06 '21 at 00:18

5

Your proof is long, but correct. If you know about binomial coefficients, you can write your polynomial as $$ x^3-6x^2+11x-6=6\binom{x-1}{3} $$ which shows that your polynomial is always divisible by $6$ for $x\in\mathbb{Z}$, and therefore, by $3$.

answered Nov 06 '21 at 00:18

robjohn

345,667

Bernard · Answer 2 · 2021-11-05T22:06:16.580

3

I think your proof is much too long. You have to show this expression is congruent to $0\bmod 3$, so use congruences, and remember that lil' Fermat asserts that $x^3\equiv x\mod 3$ for any $x$.

edited Nov 05 '21 at 22:06

answered Nov 05 '21 at 21:52

Bernard

175,478

I have updated my post with a new proof. But, I am not very confident in it. – India J. Delta Nov 08 '21 at 20:44

score 2 · Answer 3 · answered Nov 05 '21 at 21:54

2

Your proof is correct but you are going the long way to solve the problem.

Not that for an integer $x$ we have $$x^3 - 6x^2 + 11x - 6\equiv x^3-x \equiv x(x-1)(x+1) \pmod 3 $$

Thus you have three consecutive integers and one of them is a multiple of 3

answered Nov 05 '21 at 21:54

Mohammad Riazi-Kermani

68,728

I suppose that I shouldn't take $x = -1, 0, 1$ to be cases...? – India J. Delta Nov 08 '21 at 20:42

score 2 · Answer 4 · answered Nov 05 '21 at 21:55

2

I think your proof is too long, but flawless.

Because all integer is one of the $3n, 3n+1, 3n+2$ form, and you prooved at every form.

But I agree with Bernard, your proof is too long.

Basic way to proof is using $x^3-6x^2+11x-6=(x-1)(x-2)(x-3)$, and it must be multiple of 3 at $3n, 3n+1, 3n+2$ form each.

answered Nov 05 '21 at 21:55

MH.Lee

5,568

I was so wrapped up in figuring this thing out that I didn't stop to think about the simplest thing - checking the zeros. I can take those to be cases and go from there, correct? – India J. Delta Nov 05 '21 at 22:04

score 2 · Answer 5 · answered Nov 05 '21 at 22:06

I like your proof here is another alternative.

Since this is a cubic let's try completing the cube

$$x^3-6x^2+11-6 = (x-2)^3-x + 2 = (x-2)((x-2)^2-1)=(x-2)(x^2-4x+3)=(x-1)(x-2)(x-3).$$

For any $x\neq1,2,3$ Either $x-1$, $x-2$, or $x-3$ will be divisible by three since they are three consecutive numbers. Note also that at least one of the factors is even so not only is your expression divisible by 3, it's actually divisible by 6!

Show that $x^3 - 6x^2 + 11x - 6$ is divisible by $3, \forall x \in \mathbb{Z}$.

5 Answers5