Q. Prove that: If we remove 12 points from the Euclidean plane $\mathbb{R}^2$ to get set $A$, then $A$ is connected.
I don't really understand how to proceed with the question. I thought of going via contradiction but I am stuck. Should I approach it via path connectedness?
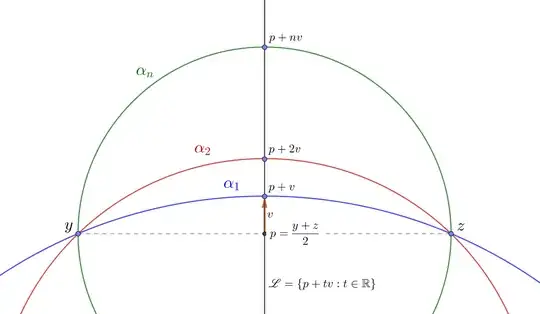
We know that if $X$ is connected by paths then $X$ is connected. If we think of a polygonal path that dribbles the n points, the test would end, but I think this way does not show what may be happening behind the scenes. I will try to give a fairly visual demonstration: So suppose that $A=\mathbb R^2\setminus\{x_1,x_2,\dots,x_k\}$ where $x_i\neq x_j$ if $i\neq j$. Let $y,z\in A$, if the line that joins $y$ with $z$ does not contain any of the points $\{x_1,x_2,\dots,x_k\}$, finish the test. Otherwise, let $p$ be the midpoint of $y$ and $z$. Let $\mathscr L=\{p+tv:t\in\mathbb R\}$ the equidistant line of points $y$ and $z$.
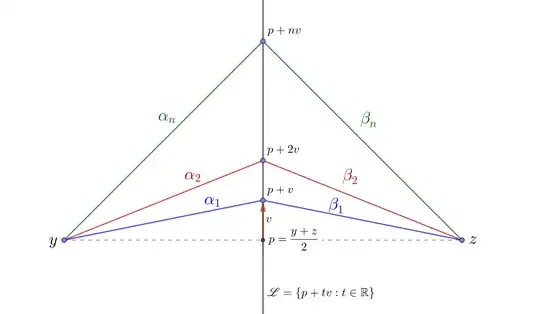
Then for each $n\in\mathbb N$ there are two lines $\alpha_n$ and $\beta_n$ that join the points $y$ with $p+nv$ and $p+nv$ with $z$, respectively. Let $\gamma_n=\alpha_n*\beta_n$ a path that $y$ with $z$. Then we notice that $\gamma_n\cap\gamma_m=\{y,z\}$ for $n\neq m$. Let's suppose $\forall n\in\mathbb N,\exists r_n\in\{1,2,\dots,k\}$ such that $x_{r_n}\in\gamma_n$, which is false since we can list the $n + 1$ first steps and have: $$ \color{red}{k+1\text{ elements}}\left\{ \begin{array}{l} \color{red}{x_{r_1}}\in\gamma_1\\ \color{red}{x_{r_2}}\in\gamma_2\\ \vdots\\ \color{red}{x_{r_k}}\in\gamma_k\\ \color{red}{x_{r_{k+1}}}\in\gamma_{n+1}\\ \end{array} \right. $$ thus there exists a point $x_r$ that belongs to two paths $\gamma's$, which is a contradiction. Therefore $\exists n_0\in\mathbb N$ such that $\{x_1,x_2,\dots,x_k\}\not\in\gamma_{n_0}$. Thus there is a path $\gamma_{n_0}$ in $\mathbb R^2\setminus\{x_1,x_2,\dots,x_k\}$ that joins point $y$ with $z$. Then $\mathbb R^2\setminus\{x_1,x_2,\dots,x_k\}$ is connected by paths, then $\mathbb R^2\setminus\{x_1,x_2,\dots,x_k\}$ is connected.
On the other hand if you want you can work with portions of circles instead of working with line segments, like this:
If you remove the whole $\mathbb{Q}^2$ (i.e. the set $\mathbb{R}^2 - \mathbb{Q}^2$), you still get a path connected set. You can find the proof of this on this website.
