Point addition on an elliptic curve

Question

I have an elliptic curve $y^2 = x^3 + 2x + 2$ over $Z_{17}$. It has order $19$.

I've been given the equation $6\cdot(5, 1) + 6\cdot(0,6)$ and the answer as $(7, 11)$ and I'm unsure how to derive that answer.

I have $6\cdot(5, 1) = (16,13)$ and $6\cdot(0,6)=(0, 11)$ however when I use point addition to add them together I get $(16,13)+(0, 11)=(14,11)$ which isn't even a point on the curve...

Could someone help me identify where and why I've gone wrong?

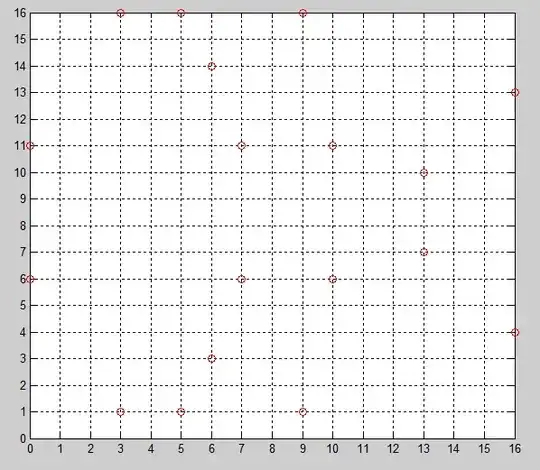
For further information here's each of the points:

enter image description here

And here's the curve plotted out: enter image description here

Amzoti · Accepted Answer · 2013-06-28T15:46:47.513

5

Hints:

Your calculation of $6(5,1) = (16,13)$ is correct.
Your calculation of $6(0,6) = (0,11)$ is incorrect, you should get $6(0,6) = (3,1)$.

Maybe if you show how you did that calculation, I can spot the issue.

Once you fix that, I verified the author's result is correct, that is:

$$(16,13)+(3,1) = (7,11)$$

Update

Here are some additional hints to help you with intermediate calculations:

$P = (0,6)$
$2P = (9,1)$
$3P = (6,3)$
$4P = (7,6)$

edited Jun 28 '13 at 15:46

answered Jun 28 '13 at 15:28

Amzoti

56,093

Thanks for this, I'll redo my working for the second one and if I'm still struggling I'll get back to you, if not then I'll accept this. – Peanut Jun 28 '13 at 15:39
@Peanut: Sounds great, I also added an update with some initial calculations, so you can verify as you are doing your calculations. Let me know if you still have issues. Regards – Amzoti Jun 28 '13 at 15:47
Thanks for the hints, just done $2P$ and it's correct so I've got the method right, must have made a silly mistake somewhere. Is there a quick way to do these, or do you just have to work out $P$ then $2P$, then $3P, 4P$ etc or can you say for example point double $2P$ to get $4P$ and skip $3P$? I've just started looking at this topic and have a programming background so have relatively little mathematical knowledge. – Peanut Jun 28 '13 at 15:59
@Peanut: In practice, you want to minimize the number of calculations you do, so yes, always minimize the number as much as is possible. Here, we can do (2P, 2.2P, 2P + 4P), or get to (3P = P + 2P, 2.3P). Clear? We are typically talking huge numbers in real life, so reductions are critical to speed. ALso, you are doing great! Regards – Amzoti Jun 28 '13 at 16:11
Yep clear enough. I've done it one at a time though just so I can get used to the method, I get $5P = (10,11)$ which is a point on the curve so looks okay but then $6P$ falls down for me as I get $(3,11)$ Working: $s=\frac{6-11}{0-10} = 2^{-1} = 9 \bmod 17$. $x = 9^2-10-0=3\bmod17$ $y=9\cdot(10-0)-11=79\bmod 17=11$ Really appreciate your help, I'll have a go at $2P + 4P$ to get $6P$. – Peanut Jun 28 '13 at 16:23
@Peanut: excellent on 5P! I will have to check the other issue, but try it the other 2P + 4P – Amzoti Jun 28 '13 at 16:46
The group of points on an elliptic curve is abelian so here you could have worked out $Q=(5,1) + (0,6)$ and then found $6Q$. This is much more efficient. – fretty Jun 28 '13 at 16:48
@Amzoti Found my own mistake, I was doing $y3 = s(x_1−x_2)−y1$ instead of taking away $x_3$ from $x_1$. Thanks so much. – Peanut Jun 28 '13 at 16:56
@Peanut: You are very welcome and I just did the calc and was going to post that! Regards! – Amzoti Jun 28 '13 at 17:03
@fretty: Point noted, thanks! I am not sure it is a good idea to introduce that just yet as there many opportunities for learning minimization techniques when doing it in real life, but it is an important observation in that regard! Regards – Amzoti Jun 28 '13 at 17:37
Well there is nothing really mysterious going on. If I asked you to calculate 61638498928 + 678270937049720, would you work out the two multiples first and then add or use the distributive law to write it as 6*(1638498928+78270937049720)? – fretty Jun 28 '13 at 17:49
@Amzoti Sorry to bother you again but I'm just trying the $4P + 2P$ and can't do it. Even getting the $s$ value is awkward. I have $2P = (9,1)$ $4P = (7,6)$ so $s = \frac{6-1}{7-9}=-\frac{5}{2}=-2^{-5}=-\frac{1}{32}=-32^{-1}$. I then get $-32x = 1\mod17$ and therefore $x=9$ meaning $s=9$. Here's where it goes wrong. $x=9^2-9-7=81-16=65\mod17=14$ whereas the x co-ordinate should be $7$. Any idea where I've gone wrong? Again, thanks for the help. – Peanut Jun 28 '13 at 17:53
@fretty In this case I already had $6\cdot(5,1)$ so didn't have to do any calculations for it but I appreciate the tip! – Peanut Jun 28 '13 at 17:57
@Peanut: Be careful with those negative numbers and modular inverses! We have $((5/(-2))^2 -9 - 7) \mod 17 = ((5 \times 8)^2 + 1) \mod 17 = 3$. Do you get the $-2$ modular inverse is equal to $8$? Please make sure you get that for $x$ first. There are many ways to do that, but go slow and then practice other ways to do it! – Amzoti Jun 28 '13 at 18:06
@Amzoti I only learnt about modular arithmetic yesterday so it's a bit confusing, I've managed fine so far with powers of $-1$ but could you just quickly explain how you got from $5/(-2)$ to $5 \times 8$? I'm just not seeing it. Promise I'll stop bothering you after this, and again, many thanks! – Peanut Jun 28 '13 at 18:24
@Peanut: It is critical to understand this! Do a small diversion, work this first and make sure you get this example: http://en.wikipedia.org/wiki/Modular_multiplicative_inverse#Example. Next do $(1/(-1), 1/(-2), 1/(-3) ... 1/(-10)) \mod 11$ (in other words, do the modular inverse of each number mod 11) and make sure you get $(1, 6, 4, 3, 9, 2, 8, 7, 5, 10)$. What do you notice? Now, try $(1/(-2)) \mod 17$. Lastly, we have $5 \times$ that modular inverse. Report back if not clear! Regards – Amzoti Jun 28 '13 at 18:32
1
1 for great hints, great follow-up, and great patience!

amWhy

Jun 29 '13 at 00:05

g'nite (soon) ;-) – amWhy Jun 29 '13 at 04:09

@Amzoti I really appreciate you walking me through this. The Wiki example is easy, and I understand how you got from $\frac{5}{−2}$ to $5\times8$ now. However for your $\mod 11$ calculations I work them all out the same as you, but as negative values? Method I've been told to use for e.g. $1/(-1)$ we do $-1(x) = 1\mod11$ What value does $x$ have to take to make $-1(x) = 1$? It could be either $-1 (-1\times-1 = 1\mod11)$ or $10 (-1\times10 = -10 = 1\mod11)$. Obviously there's something wrong in my method... I can post this as a separate question if you're sick of helping, no worries. Thanks. – Peanut Jul 01 '13 at 12:14

It is okay to have negatives as long as you mod them again and get the correct positive number. For example $-1 \pmod {11} = 10 \pmod {11}$. If all of them work out like that, you are okay. Rgeards – Amzoti Jul 01 '13 at 12:41

score 2 · Answer 2 · answered Jun 28 '13 at 19:20

You can aid (read: double-check) your calculations with the computer, for instance using Sage or Magma. For example, you can use for free the Magma online calculator. The following code defines your curve $E$ over $\mathbb{Z}/17\mathbb{Z}$, and calculates $6\cdot (0,6)$.

g:=GF(17).1;

E:=EllipticCurve([0,0,0,2*g,2*g]);

P:=E![0,6];

6*P;

The output is $[3:1:1]$ which are projective coordinates for the point $(3,1)$, as it should be.

Point addition on an elliptic curve

2 Answers2

Linked