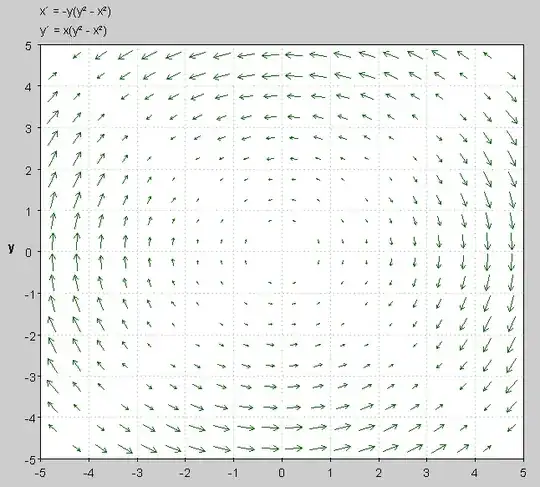
We are given the system:
$$x' = -y ( y ^{2} - x^{2})$$ $$y' = x ( y ^{2} - x^{2})$$
How we can find the critical points of this problem?
Additionally, how we can study the stability of first and second bisector?
Asked
Active
Viewed 131 times
1
-
There is my auestion. how we can study the stability of first and second bisector – Vrouvrou Jun 30 '13 at 13:38
-
the first bisector is $y=x$ and the second is $y=-x$ – Vrouvrou Jun 30 '13 at 13:44
-
Where did this problem come from (what book)? – Amzoti Jun 30 '13 at 14:02
-
A related problem. – Mhenni Benghorbal Jun 30 '13 at 14:18
1 Answers
5
To find the critical points, you want to find the points where $x'$ and $y'$ are simultaneously equal to zero.
We are given:
$$f(x, y) = x' = -y ( y ^{2} - x^{2})$$ $$g(x, y) = y' = x ( y ^{2} - x^{2})$$
When we simultaneously set and solve $x' = 0$ and $y' = 0$, we get:
$$(x,y) = (0,0), x = y, x = -y$$
So, now we have a zero critical point, and a first and second bisector as you call them.
Next, we find the Jacobian matrix of the system as:
$$\displaystyle J = \begin{bmatrix} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y}\\\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y}\end{bmatrix} = \begin{bmatrix}2xy & -3y^2+x^2\\y^2-3x^2 & 2xy\end{bmatrix}$$
Now, evaluate the eigenvalues of Jacobian matrix of those three critical point (point and two bisectors). What sort of solution do you get when you vary the values for those bisectors?
It looks menacing, but you will that for different $x = y, x = - y$, the Jacobian reveals a phase portrait that is split along those bisectors. For example:
Amzoti
- 56,093
-
-
Here too...empty. I wish I knew in advance if and when traffic picks up! – amWhy Jul 01 '13 at 02:32