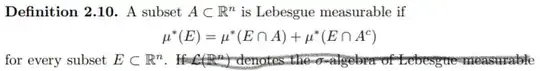0

I got a little confused with the relationship of those two concepts while reading a text of J.K. Hunter in which he's defined them as follows;

Caratheodory measurable sets

enter image description here

Lebesgue measurable sets

enter image description here

Question

In Thr 2.4 on the text, we also studied that Lebesgue outer measure is an outer measure. So, now, I can't seem to figure out what the def of Lebesgue measurable sets adds to the def of Caratheodory measurable sets..

Can anyone help me with it?

Supplementary

I also went through a couple of MathSE articles regarding this but no luck yet...

Rowing0914
  • 634
  • 3
    The definition 2.10 only says that "Lebesgue-measurable" is a shorthand for "Carathéodory-measurable with respecto to the Lebesgue outer measure". – azif00 Dec 20 '21 at 01:24
  • The sets that satisfy the Caratheodory measurability condition form a $\sigma$-algebra, exactly what you want to do integration on abstract spaces. The utility of the construction is that any premeasure on an algebra of subsets of a space $X$ induces an outer measure, to which the construction then applies. And premeasures and algebras are easier to define (and visualize). For example, on $\mathbb R$ take the algebra of $\textit{finite}$ unions of intervals and define a premeasure on these as sums of lengths of disjoint intervals. From this, Lebesgue measure follows more or less automatically. – Matematleta Dec 20 '21 at 01:51
  • Definition 2.8 does not seem right. It never says what $E$ is. – 311411 Dec 20 '21 at 03:12
  • 1
    Lebesgue measurable sets are just Caratheodory measurable sets with respect to the Lebesgue outer measure. – Ramiro Dec 20 '21 at 03:29
  • @azif00, and Ramiro. Thank you! "Lebesgue measurable sets are just Caratheodory measurable sets with respect to the Lebesgue outer measure" makes sense!! – Rowing0914 Dec 20 '21 at 22:53
  • @Matematleta, thank you for the detailed explanation! It's a bit advanced for me since I haven't learnt premeasure yet but will come back this later!! – Rowing0914 Dec 20 '21 at 22:54
  • @311411, I think it was defined before the Def but other answers already cleared my answer so no worries! – Rowing0914 Dec 20 '21 at 22:55
  • 1
    Rowing: good luck to you studying M.T. It can be daunting, but it sure is nifty stuff. – 311411 Dec 20 '21 at 23:11

0 Answers0