What are the number of ways two knights can be placed on a k×k chessboard so that they do not attack each other?
For k from 1 to 8, the answer is given below.
0
6
28
96
252
550
1056
1848
I know the answer to this problem as well as the method which I found from Number of ways two knights can be placed such that they don't attack.
But, I tried it using a different method and wanted to know the problem with my method. Here is what I did
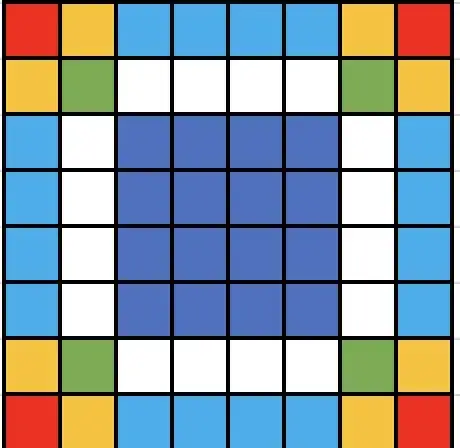
The Dark Blue Squares in the middle (k-4)x(k-4) chess boards, if we select the first knight in this square, then we can select the other knight so that they don't attack each other in $(k^2-8)$ ways. So, in total $(k-4)^2.(k^2-8)$
Now, the light blue squares (the squared in the border region), there are $4.(k-4)$ such squares, and if we select our first knight from here, then the second knight can be selected in $(k^2-4)$ ways. So, in total $4.(k-4).(k^2-4)$.
Now, the white squares, there are $4.(k-4)$ such squares, and if we select our first knight from here, then the second knight can be selected in $(k^2-6)$ ways. So, in total $4.(k-4).(k^2-6)$.
Now, the red squares (corner ones), there are $4$ such squares, and if we select our first knight from here, then the second knight can be selected in $(k^2-2)$ ways. So, in total $4.(k^2-2)$.
Now, for the squares adjacent to the corner (yellow ones), there are $8$ such squares, and if we select our first knight from here, then the second knight can be selected in $(k^2-3)$ ways. So, in total $8.(k^2-3)$.
Now, at last for the square diagonally adjacent to the corner square (green ones), there are $4$ such squares, and if we select our first knight from here, then the second knight can be selected in $(k^2-4)$ ways. So, in total $4.(k^2-4)$.
Using this process we will double count our square exactly one, so our final answer will be half of this.
So, in total the number of ways is $\frac{(k-4)^2.(k^2-8)+4.(k-4).(k^2-4)+4.(k-4).(k^2-6)+4.(k^2-2)+8.(k^2-3)+4.(k^2-4)}{2}$.
But, this gives the wrong answers, like for k=8, it gives 1880, but it should give 1848, and so on. I think there might be triple counting somewhere, but I don't understand how this could be the case as my first square is selected from different zones.
Edit: I found the mistake in my method, it was a silly error, When I am excluding the positions where I can't place my knights, I didn't exclude the position where I already place the knight. So, say for the middle dark blue zone the total ways is $(k-4)^2.(k^2-9)$ and not $(k-4)^2.(k^2-8)$. And so on for others, using this I found my answer to match the correct answer.