I'm learning to calculate limits in high school and at some point in the class we stumbled upon this exercise:
$$\lim\limits_{x\to 0} \frac{e^{2x}-1}{3x}$$
I know that I could use L'Hôpital's rule to solve it, but I'm curious if there's any other way to solve this limit, since not even my professor could think of a way.
To prove it, I use a Sandwich-type argument by usually first proving (in class) that $$\lim_{x\to 0}\frac{e^x-1}{x}=1.$$ Indeed by Bernoulli's inequality I $$e^x-1\geq (1+x)-1=x.$$ Now since $x^n\leq x^2$ for $-1\leq x\leq 1$ and $n\geq 2$ we have that \begin{align*}e^x=\lim_{n\to\infty}\left(1+\frac{x}{n}\right)^n&=\lim_{n\to\infty}\sum_{k=0}^n{n\choose k}\frac{x^k}{n^k}\\ &=\lim_{n\to\infty}1+x+\sum_{k=2}^n{n\choose k}\frac{x^k}{n^k}\\ &\leq \lim_{n\to\infty}1+x+\sum_{k=2}^n{n\choose k}\frac{x^{\color{red}2}}{n^k}\\ &= \lim_{n\to\infty}1+x+\left(\sum_{k=2}^n{n\choose k}\frac{1}{n^k}\right)\cdot x^2\\ &= \lim_{n\to\infty}1+x+\left(\left(1+\frac{1}{n}\right)^n-2\right)\cdot x^2\\ &= 1+x+\left(e-2\right)\cdot x^2 \end{align*} and by plugging these I get the limit.
Once this is taken care of your result is a simple variable change.
$$\lim_{x\rightarrow 0} \frac{e^{2x} - 1}{3x}=\lim_{x\rightarrow 0} \frac{e^{2x} - 1}{2x}\cdot\frac 2 3=\frac 2 3 \cdot \underbrace{\lim_{u\rightarrow 0}\frac{e^u-1}{u}}_{\text{derivative of exp}}=\frac 2 3$$
You can make use of the series representation of $e^x$ $$ e^x = 1 + x + \frac{x^2}{2!}+ \cdots $$ So $$ \begin{aligned} \lim\limits_{x\to 0} \frac{e^{2x}-1}{3x} &= \lim\limits_{x\to 0} \frac{1+(2x) + \frac{(2x)^2}{2!}+\cdots-1}{3x}\\ &= \lim\limits_{x\to 0} \left( \frac{2}{3}+\frac{4x}{6}+\text{terms in higher powers of x} \right) \\ &= \frac{2}{3} \end{aligned} $$
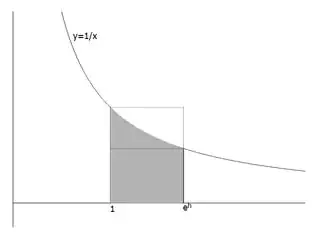
I think if you've seen the definition of the derivative, this question usually wants you to recognize the connection between the derivative of $e^x$ at $0$ and the $\lim\limits_{x\to 0} \frac{e^x-1}{x}$, but I believe if you know the definition of the natural logarithm and that the exponential function is it's inverse, there is a geometric argument based simply on the graph of $y=1/x$ below which doesn't actually use calculus. Note that the area of the shaded region is $h$, so
$$ (e^h-1)\cdot 1\ge h\ge (e^h-1)\cdot e^{-h}$$ $$ 1\ge \frac{h}{e^h-1}\ge e^{-h}$$ $$ 1\le \frac{e^h-1}{h}\le e^{h}$$
Now let $h\to 0$. Of course you have to have factored the numerator and taken out the constant factor from your original expression as discussed in the comments.
I guess that really only gets you ${h\to 0^+}$, but it shouldn't be too hard to fix.
Let me add one more answer. $$\lim_{x\to0}(1+x)^{1/x}=e$$ Taking $\log$ on both sides: $$\lim_{x\to0}\frac{\ln(1+x)}x=1$$ Substituting $x$ with $e^t-1$: $$\lim_{t\to0}\frac{t}{e^t-1}=1$$ Finally: $$\lim_{x\to0}\frac{e^{2x}-1}{3x}=\frac23\lim_{x\to0}\frac{e^{2x}-1}{2x}=\frac23\lim_{x\to0}\frac{e^{t}-1}{t}=\frac23$$
