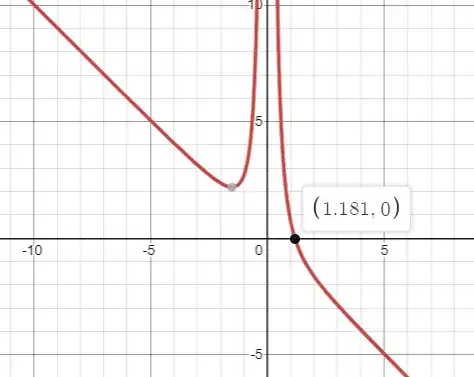
Question: $$\frac{x}{\sqrt{x^2+1}} = x^4 - x$$
I tried: $$\rightarrow \frac{1}{\sqrt{x^2+1}} = x^ 3 - 1$$
$$\to\frac{\sqrt{x^2 + 1}+1}{\sqrt{x^2+1}} = x^3$$
Now rationalising it $$\to \frac{x^2 +1-1}{x^2+1-\sqrt{x^2+1}} = x^3$$
$$\frac{1}{x^2+1-\sqrt{x^2+1}} = x$$
Can we do anything with this? How to solve? Please help me.