How do I map a Sphere to a Sphube (a special Superellipsoid)?

Question

UPDATE: I realized the formula actually works fine (once I started using $2/r$ instead of $r$), but the mesh I was working with was not a perfect sphere to begin with, which led to skewed results, as you can see in the last screenshot I posted.

I'm trying to programmatically create a superellipsoid (specifically a "sphube") in a 3D program (Blender, using geometry nodes) for which I define the flattening.

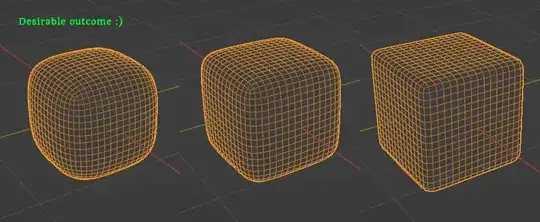
I want to end up with something resembling these:

[

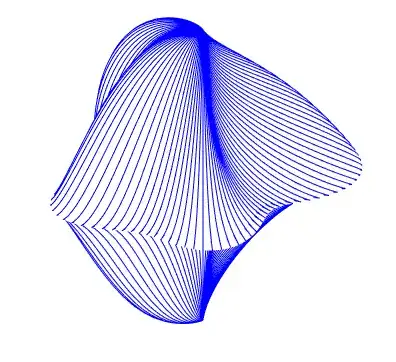
With the formula I came up with, I'm getting these instead:

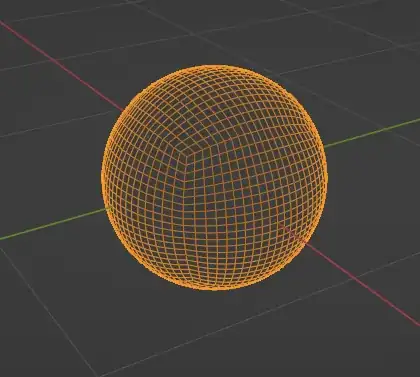
Let me walk you through my process. I start with a sphere with a radius of 1:

This is the formula I'm using to define the points on the surface of my sphube:

$$\lvert x\rvert^r + \lvert y\rvert^r + \lvert z\rvert^r = 1$$

Where x, y and z are the coordinates of each vertex and r is a real positive number (supposedly between 0 and 1) that controls the amount of flattening at the tips and the equator.

My thought process goes like this: I want to find a factor f with which to multiply each point's vector from the sphere's origin [0,0,0], so that each point lands on the sphube with the given flattening r. This is the formula I end up with:

$$(\lvert x\rvert * f)^r + (\lvert y\rvert * f)^r + (\lvert z\rvert * f)^r = 1$$

I solve for f as follows:

$$(\lvert x\rvert^r * f^r) + (\lvert y\rvert^r * f^r) + (\lvert z\rvert^r * f^r) = 1$$

I divide both sides by $f^r$ and switch sides:

$$\frac{1}{f^r} = \lvert x\rvert^r + \lvert y\rvert^r + \lvert z\rvert^r$$

I flip it (or whatever the correct term may be):

$$f^r = \frac{1}{\lvert x\rvert^r + \lvert y\rvert^r + \lvert z\rvert^r}$$

I take the r-th root:

$$f = \frac{1}{\sqrt[r]{\lvert x\rvert^r + \lvert y\rvert^r + \lvert z\rvert^r}}$$

As mentioned above, I multiply each point of my initial sphere with the computed f, but get the star-like results shown above. Since the vectors are obviously going in the wrong direction, I tried dividing, instead, and I get this:

This is more like it, but the edges are pointed, instead of rounded, and the centers of the squares are bulged. And no value of r is giving me a perfect cube. So that can't be it either, can it?

Can anyone tell me where I'm going wrong? Or, alternatively provide me with a clean formula to map a sphere (or a cube) to a sphube (even if it worked correctly, the method I'm using will result in skewed vertices towards the edges)?

Thanks!

Answer 1

I believe that I can offer an alternative approach that I have used successfully for several years. The idea is to use an extension of the idea of a body of revolution, albeit for revolution about a non-circular closed curve. But first things first.

So, first you need to define the vertical and horizontal curves you will be using. I have developed something I call superconics that will do this very well, and I have described it here. You will see that it can give you squarish circles, but a great many additional opportunities.

The next step is to develop the spherical product. This term does not appear in the mathematical lexicon, but is widely used in computer graphics. Mathematically, it is expressed as

$$ s\left( u,v \right)=h\left( v \right)\otimes g\left( u \right) $$

where $s\left( u,v \right)$ is the surface composed of vertical curves $h\left( v \right)$ around a closed planiform curve $g\left( u \right)$ and $u$ is the longitude ($0\le u\le2\pi$) and $v$ is the latitude ($\pi/2\le v\le\pi/2$).

Now, apologies here, because I do almost everything in complex variables, So, if you express $h\left( v \right)$ and $g\left( u \right)$ in complex variables, then the components of the spherical product, that is, the matrix $s$, are given by

$$ \begin{align} & {{s}_{x}}\left( u,v \right)= & \operatorname{Re}\left\{ h\left( v \right) \right\}\,\operatorname{Re}\left\{ g\left( u \right) \right\} \\ & {{s}_{y}}\left( u,v \right)= & \operatorname{Re}\left\{ h\left( v \right) \right\}\,\operatorname{Im}\left\{ g\left( u \right) \right\} \\ & {{s}_{z}}\left( u,v \right)= & \operatorname{Im}\left\{ h\left( v \right) \right\} \end{align} $$

I suppose that in Cartesian coordinates you would just replace $(\operatorname{Re},\operatorname{Im})$ by $(\cos,\sin)$. I have implemented the spherical product in Matlab with a very minor modification of the sphere function, if you are familar with that.

Carrying this a bit further, I've generalized the spherical product to calculate three-dimensional bodies of arbitrary (i.e., non-circular) revolution with essentially any vertical and horizontal profiles. Th animation below shows such a 'body of revolution' with an arbitrary planiform and variable longitude lines