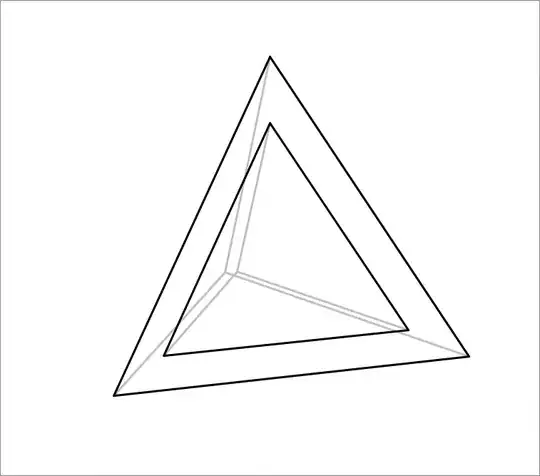
Given a regular tetrahedron, make a uniformly scaled copy of it, such that both the original and the scaled copy (the scale factor is less than $1$) share the same centroid, and have the same orientation. Then rotate the scaled copy such that its four vertices lie on the four faces of the original tetrahedron.
Suppose the scale factor is specified, what would be involved in finding the rotation matrix that when applied to the scaled down tetrahedron gives the desired result of inscribing it in the original tetrahedron?
Has this problem been studied? Any citations, pointers, or hints are greatly appreciated.
EDIT: The range for the scale factor is $ \dfrac{1}{3} \le f \lt 1 $