Introduction:
For some background information on the Dottie Number D, see the great posts at:
Some definitions:
The “solution” to Kepler’s equation is Kepler E:
$$M=E-e\sin(E)\iff x=y-a\sin(y)\implies y=\text E(a,x)$$
and Inverse Beta Regularized function $\text I^{-1}_z(a,b)$, Beta Regularized function $\text I_z(a,b)$, and the Incomplete Beta function $\text B_z(a,b)$:
$$\text B_z(a,b)=\int_0^z t^{a-1} (1-t)^{b-1}dt, \text I_z(a,b)=\frac{\int_0^z t^{a-1} (1-t)^{b-1}dt}{\int_0^1 t^{a-1} (1-t)^{b-1}dt } =\frac{\text B_z(a,b)}{\text B(a,b)}$$
$$\text I_y(a,b)=z\implies y=\text I^{-1}_{0\le z\le 1}(a\ge 0,b\ge0)=\text I^{-1}_z(a,b)$$
where the restrictions on $z,a,b$ help find the quantile of a Beta type Distribution. The goal is to notice that:
$$\text B_z\left(\frac12,\frac32\right)=\int_0^z \sqrt{\frac 1x-1}dx=\sqrt{x-x^2}+\sin^{-1}\sqrt x\implies \text B_{\sin^2(z)}\left(\frac12,\frac32\right)\mathop=^{0\le z\le \frac\pi2}z+\sin(z)\cos(z)=z+\frac12 \sin(2z)$$
and $$z+\frac12 \sin(2z)=y\mathop=^{x=2z} \frac x2+\frac 12 \sin(x)=y\implies x-(-\sin(x))=2y\implies x=\text E(-1,2y)\implies z=\frac {\text E(-1,2y)}2$$
while the dottie number:
$$x=\text D:x-\cos(x)=0\mathop\implies^{x=\frac \pi2-z}\frac \pi2-z-\cos\left(\frac\pi2-z\right)=\frac\pi2-z-\sin(z)=0\implies \frac \pi2=z-(-\sin(z))\implies z=\text E\left(-1,\frac\pi2\right)=\frac\pi 2-x\implies \frac\pi2-\text E\left(-1,\frac\pi2\right) =x$$
However if $$\text B_{\sin^2(z)}\left(\frac12,\frac32\right)=z+\frac12 \sin(2z)=\text B\left(\frac12,\frac32\right) \text I_{\sin^2(z)}\left(\frac12,\frac32\right)=\frac \pi2 \text I_{\sin^2(z)}\left(\frac12,\frac32\right)=y \implies \sin^2(z)=\text I^{-1}_{\frac{2y}\pi}\left(\frac12,\frac32\right)\mathop\implies^{0\le z\le\frac \pi 2} \sin^{-1}\sqrt{\text I^{-1}_{\frac{2y}\pi}\left(\frac12,\frac32\right)}=z$$
Therefore:
$$\text E(-1,x)=2\sin^{-1}\sqrt{\text I^{-1}_{\frac x\pi}\left(\frac12,\frac32\right)}=\text{hav}^{-1}\left(\text I^{-1}_{\frac x\pi}\left(\frac12,\frac32\right)\right)\,\implies \text I^{-1}_x\left(\frac12,\frac32\right)= \sin^2\left(\frac{\text E(-1,\pi x)}2\right)=\text {hav}(\text E(-1,x))$$
where appears the Half Versed Sine and Inverse Half Versed Sine
Therefore:
$$\text D= \frac\pi2-\text E\left(-1,\frac\pi2\right) =\frac \pi2-2\sin^{-1}\sqrt{\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)}=\sin^{-1}\left(1-2 \text I^{-1}_\frac12\left(\frac 12,\frac 32\right)\right) $$
which is the Inverse Half Covered Sine. Using $\text D=\cos^{-1}(\text D)$ we get a perfect approximation with this computation and another closed form:
The Main Result: $$\boxed{\text{Dottie Number}=\text D=\text{hacoversin}^{-1}\,\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)=2\sqrt{\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)-\text I^{-1}_\frac12\left(\frac 12,\frac 32\right)^2}}$$
where $\sqrt{\text{quantile}(1-\text{quantile})}$ is not quite a statistical formula and where the arcsin formula works with an error of $10^{-179}$. Also, $\text I^{-1}_\frac12(a,b)$ finds the median of a Beta Distribution with $a,b$ as shape parameters.
The Question:
Even though the calculations are an explanation,
what is the intuition behind the Dottie number being the inverse half covered sine of the median of a Beta distribution with half integer shape parameters?
Phrased differently, why is the dottie number the positive square root of $x-x^2$ where $x$ is the median of a Beta distribution with half integer shape parameters?
Please correct me and give me feedback!
Side Note $1$:
Therefore we have a closed form for a Inverse Beta Regularized function special case:
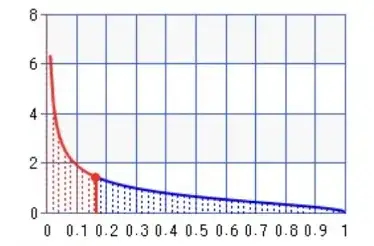
Median of $\frac 2\pi \sqrt{\frac 1x-1}$:
where the median is the point such that half of the area of a curve is the red region and the other half is the blue region. The $\color{red}{\text {red}}$ horizontal line is the median:
$$\text{median}=\text I^{-1}_\frac12\left(\frac12,\frac32\right)=\frac {\text D_\text{DHA}^2}4=\text{hacoversin}(\text D)= \frac{1-\sqrt{1-\text D^2}}2=0.16319398540839259232…\implies \int_0^{\frac {\text D_\text{DHA}^2}4} \sqrt{\frac1x-1}\,dx=\int_0^{\text I^{-1}_\frac12\left(\frac12,\frac32\right)} \sqrt{\frac1x-1}\,dx=\frac\pi4 $$
where $\text D_\text{DHA}= \sqrt{1+\text D} - \sqrt{1-\text D} = \sqrt 2\sqrt{1-\sqrt{1-\text D^2}} $ is the offset at which $2$ unit disks overlap by half of each’s area constant
Notice how the dottie number appears in the offset when a unit disk is half over another one and the median, where the areas from $0$ to the median is half of the area under the curve, of a beta distribution.
Side Note $2$:
Let use The power series expansion of $\text I^{-1}_z(a,b)$ about $z=0$:
$$\text I^{-1}_z(a,b)\mathop=^{a>0}(az\text B(a,b))^\frac1a+\frac{b-1}{a+1} (az\text B(a,b))^\frac 2a+ \frac{(b-1)(a^2+3ab-a+5b-4}{2(a+1)^2(a+2)}(az\text B(a,b))^\frac 3a +…$$
to get another series expansion of the dottie number:
$$\text D=\text{hacoversin}^{-1}\left(\frac{\pi^2}{64}+\frac{\pi^4}{12288}+ \frac{11\pi^6}{11796480}+ \frac{\pi^8}{20643840}+…\right)=\sqrt{1-\left(-1+2\sum_{n=1}^\infty a_n \pi^{2n}\right)^2}$$
which correct to $3$ decimal places by $4$ terms where $a_n$ may not have a closed form.