Why do we multiply in tree diagrams?

Question

In probability, we always lay out the events through tree to see what depends on what. Then we were taught to "multiply" through that branch to get the probability of that event.

Why do we "multiply"? I've noticed we have the same sort of rule in calculus too (chain rule)

EDIT: I think my question was misinterpreted. I am asking just because we put a number (usually - if not almost fractional) beside a branch, why must we "multiply" through that number or that "thing" if I am being more abstract. Where "thing" could even mean a derivative operator $$\partial / \partial x$$

Answer 1

The branch that goes from $R$ to $A$ has $1/3$ beside it. As you know, the $1/3$ means that if we are at $R$, we have probability $1/3$ of going to $A$. The $5/8$ and $3/8$ mean that if we have reached node $A$, we have probability $5/8$ of going to $D$, and probability $3/8$ of going to $E$. Let's stop here, though if you want to make the thing more tree-like, go ahead.

Now imagine say $1200$ people starting at $R$. They split along the $3$ branches coming out of $R$, with $1/3$ of them going to $A$, $1/6$ of them to $B$, and $1/2$ to $C$.

In particular, $400$ of them end up at $A$.

Now at $A$ they split, some going to $D$ and some to $E$, according to the probabilities written on the branches. So $5/8$ of the $400$ people end up at $D$. This is $250$ people.

Note that $250=(1200)(1/3)(5/8)=(1200)(5/24)$. So to determine what fraction of the $1200$ end up at $C$, we multiply $1/3$ by $5/8$.

When we are dealing with probabilities, the number who go to $A$ need not be exactly $400$, but the multiplication of probabilities takes place for essentially the same reason as in our people example.

---

diagram code:

\documentclass[11pt]{standalone}
\usepackage{tikz-cd}
\begin{document}
\begin{tikzcd}[column sep=0.3in,row sep=0.5in]
{}& & & R \ar[-]{d}[swap]{\frac{1}{6}} \ar[-]{lld}[swap]{\frac{1}{3}} 
\ar[-]{rrd}{\frac{1}{2}} & & \\
& A\ar[-]{ld}[swap]{\frac{5}{8}}\ar[-]{rd}{\frac{3}{8}} & & B &\hphantom{E} & C\\
D & & E
\end{tikzcd}
\end{document}

Remark: There is a strong analogy between the above situation, and the Chain Rule for differentiation. Let's stick to depth $2$, where we have $y=f(u)$ and $u=g(x)$. If we want the rate of change of $y$ with respect to $x$, we want to know the local scaling factor of $f(g(x)$ if we increase $x$ by a small amount $\Delta x$. What happens is that $u$ increases by about $\Delta u= (\Delta x)\frac{du}{dx}$, and $f(u)$ therefore increases by about $\Delta u \frac{dy}{du}$, that is, $(\Delta x)\frac{dy}{du}\frac{du}{dx}$.

So $\Delta x$ in a sense playes the same role as the $1200$ people did in the example above. In each case, we have a form of combined scalings. The question does a service in bringing out the analogy!

Answer 2

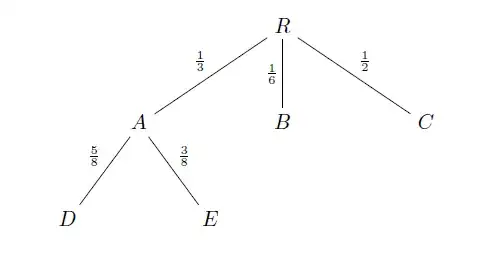
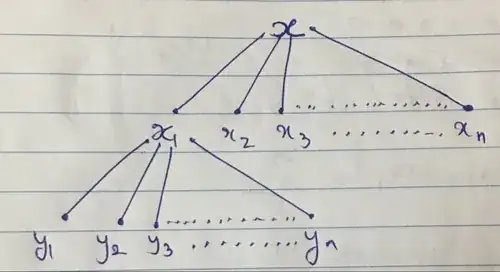
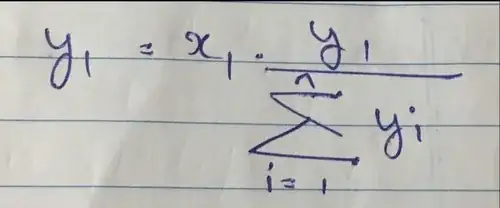
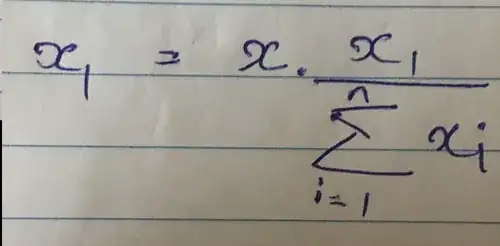Think of it this way for $P(A\cap B\cap C\cap D\cap\cdots)$.

$P(A)$ is the portion of the time that $A$ happens, and we must toss out the complementary portion, since otherwise, $A,B,C,D,E,...$ can't all happen.

$P(B\mid A)$ is the portion of the time that $B$ happens, given that we know $A$ happens, and we must toss out the complementary portion (the portion of the time that $A$ happens and that $B$ doesn't), since otherwise, $A,B,C,D,E,...$ can't all happen.

$P(C\mid A\cap B)$ is the portion of the time that $C$ happens, given that we know $A$ and $B$ happen, and we must toss out the complementary portion (when $A$ and $B$ happen but $C$ doesn't), since otherwise, $A,B,C,D,E,...$ can't all happen.

$P(D\mid A\cap B\cap C)$ is the portion of the time that $D$ happens, given that we know $A,$ $B,$ and $C$ happen, and we must toss out the complementary portion (when $A,$ $B,$ and $C,$ happen, but $D$ doesn't), since otherwise, $A,B,C,D,E,...$ can't all happen. (And so on....)

When we talk about a fraction of a thing, we mean a fraction times a thing. So, to get the probability that $A,B,C,D,...$ all happen, we multiply all the probabilities in the chain together.

---

For a more concrete example: $80\%$ of my socks are cotton, $50\%$ of my cotton socks are knee socks, $25\%$ of my cotton knee socks are white, and I use $90\%$ of my white cotton knee socks as gym socks. I have $100$ pairs of socks. How many white cotton knee socks do I use as gym socks? Well, to start with, we can toss out $20$ pairs for not being cotton (leaving $80,$ or $80\%$ of the original amount). We can toss out $40$ of the remaining pairs for not being knee socks (leaving $40,$ or $50\%$ of $80\%$ of the original amount). We can toss out $30$ of the remaining pairs for not being white (leaving $10,$ or $25\%$ of $50\%$ of $80\%$ of the original amount). Finally, we toss out $1$ more pair for not being used as gym socks (leaving us with $9,$ or $90\%$ of $25\%$ of $50\%$ of $80\%$ of the original amount).

Of course, we could get there in different ways. For example: $18\%$ of my socks are used as gym socks, $100\%$ of my gym socks are cotton, $100\%$ of my cotton gym socks are white, $50\%$ of my white cotton gym socks are knee socks. Same result.

Answer 3

I want to work out what proportion of my socks are pink socks with holes in. I might reasonably start by gathering together all of my socks, and working out what proportion of them are pink (let's say 30%); then I'll work out what proportion of pink socks have holes in (say 40%). Does it seem reasonable to say that the proportion of my socks that are pink and have holes is 40% of 30%, i.e. 12%, of my socks?

Answer 4

This question has been bothering me for a while, most of the solutions state the analogies and examples so I am trying to provide a more generalized and mathematical approach.

Consider a generic tree (not a probability tree) as shown above, where value at root is equal to sum of all the values of its branches.

X is a parent of X1, which means its value of some fraction of X. X1 equals X times the ratio of X1 to sum of all its sibling nodes.

Y1 is child node of X1, so similiary it can be written as above.

Substituting the value of X1 in above equation gives represtation of Y1 in terms of X.

I would like to point out that traversing branches is not multiplication, it is division of root value in some fraction. however in case of probability, sum of all branches equlas to 1 and we do not explicitly show X1 + X2 + .... + Xn = 1 and ignore the denominator.

Consider the following example, it shows when x=1 why it is actually division but interpreted as multiplication in practical probability. If x is not 1,it still holds for a regular tree.