5

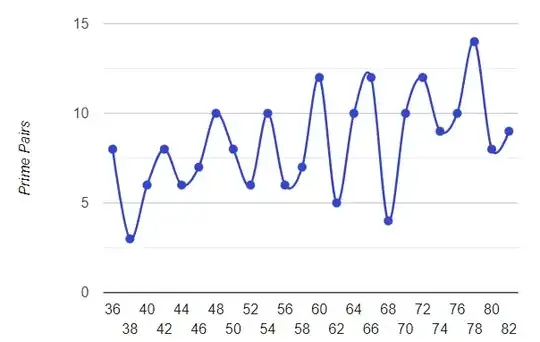
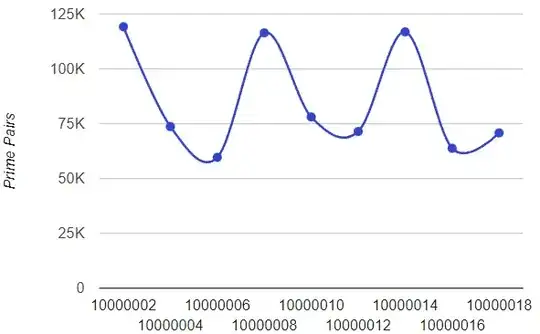
Noticed a pattern for $n \geq 6$, the number of prime pairs $(p,q)$ where $p+q=6n$, is always greater than the pairs for $6n+2$ and $6n+4$.

For example, when $n=6$

$36$ has $8$ prime pairs

(5,31) (7,29) (13,23) (17,19) (19,17) (23,13) (29,7) (31,5)

$38$ has $3$ prime pairs

(7,31) (19,19) (31,7)

$40$ has $6$ prime pairs

(3,37) (11,29) (17,23) (23,17) (29,11) (37,3)

The charts below show peaks for $6n$ and troughs for $6n+2$ and $6n+4$

primePairs

This pattern seems to continue indefinitely ...

primePairs10mil

Question

Does this pattern hold true for all $6n$ peaks?

vengy
  • 1,903
  • 1
    I think this might have to do with the fact that primes are always 1 or 5 mod 6. If we separate them into 2 categories, we take one from each category to get a sum 6n, but we need to take 2 from 1 category to get 6n+2 or 6n+4. – Fatso Boo Apr 04 '22 at 14:23
  • 5
    Dirichlet tells us that, on average, a prime is equally likely to be either $\pm 1 \pmod 6$. Thus a randomly selected pair sums to $6n$ with probability $\frac 12$, and to $6n\pm 2$ with probability $\frac 14$ each. – lulu Apr 04 '22 at 14:32
  • Here you might find the answer: https://mathoverflow.net/questions/54259/why-are-goldbach-laggards-biased-towards-2-bmod-6 – user140242 Apr 06 '22 at 17:35

1 Answers1

3

As a few commentors have pointed out, a prime is either $1$ or $5$ (mod $6$), and single prime has a ~$50$% of being in either group. Thus, we only need one of each to get a sum of $6n$, but we need two numbers that are equal (mod $6$) to get $6n+2$ or $6n+4$ (only a $25$% chance).

The specifics of your question have likely been worked out here. You have found a cool visual way to see this!

Clyde Kertzer
  • 2,904