1

Trying to solve this from a different approach now. started out here Calculate half life of esters

Is there a way to find a function that fits the graph below?

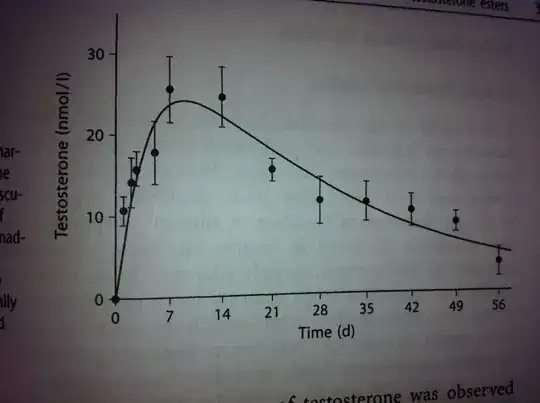
Terminal halflife of testosterone-u

There are a few criterions. The area of the graph must be A The peak of the graph must be at X (7-8 in the image) The halflife after the peak must be H

The area in this case is the amount of testosterone, or rather the injected dose. The peak is when the compound is fully absorbed.

y = f(A,X,H, t)

Is this possible?

My math skills are way too limited here

Community
  • 1
Roger Johansson
  • 163
  • What you call "half life" is used in relation with some radioactive elements which, I believe, is not your thing here, so what do you call "half life" to? The mean value of the function over the given interval? Which btw I again ask: is it $,[0,56];$ or something else? – DonAntonio Jul 15 '13 at 08:39
  • It's "terminal half life" - "Terminal plasma half-life is the time required to divide the plasma concentration by two after reaching pseudo-equilibrium" .. so in this case, from day 7 and forward.. serum levels have halved here from day 7 to day 35ish . so terminal halflife here is 28 days – Roger Johansson Jul 15 '13 at 08:42
  • http://www.fvet.uba.ar/equinos/8313/half-life.pdf contains some math for it, sadly , I don't understand anything of it :-( – Roger Johansson Jul 15 '13 at 08:52
  • Any reaction to the answer below? Nearly two years should suffice to meditate on it, no? – Did May 01 '16 at 21:44

1 Answers1

1

A first idea is to try to fit a gamma function, in your case $f(x)=sx\mathrm e^{-x/m}$. The slope at the origin is $s$, the maximum is at $x=m$ and its value is $sm/\mathrm e$.

A caveat though: which parameters of the curve are important to you is not quite clear from your question but a general principle is that the more characteristics of the curve are imposed the more parameters are needed. In the present case, slope at the origin + location of the maximum + maximal height + area under the curve would a priori need four parameters (and the gamma family above is described by only two).

Did
  • 279,727