3

This might be a bit too "hand-wavy" for this forum but here it goes:

Generally the problem is this, I wish to create a function $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$ with some properties that I have "some notion" of inside of my head. Things like I want $f$ to:

  • grow quadratically in "this" direction.
  • decrease linearly in "this" direction.
  • go towards 0 in this direction.

Sometimes capturing these ideas in a function is simple and sometimes it is not. So my question is this: what are some good methodologies for creating explicit equations for functions you picture in your head?

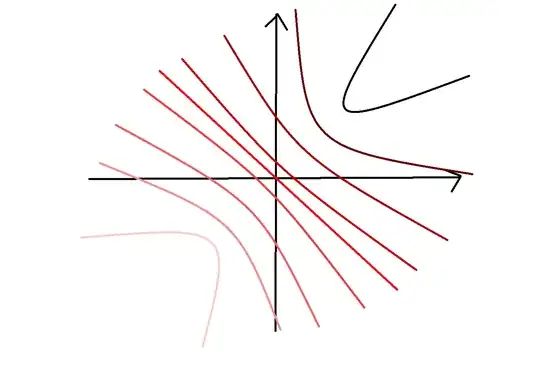
EXAMPLE

In paint I can draw the scalar field lines, or lines of constant potential energy, of an electric field I want the explicit formula of. To go from the explicit formulation of the scalar field to the electric field is simple, the problem is the explicit formulation of the scalar field represented below for instance. How would you do it?

Example scalar field that needs an explicit formulation. Lines of constant potential energy shown in varying shades of red.

Taylor Rendon
  • 2,276
Ivar Eriksson
  • 133

1 Answers1

1

Maybe a good tool to have in the toolbox is the multiplication of the $\tanh$ function to terms which represent the behavior you want.

For example, when $m=n=1$ a function which grows linearly in the negative direction and grows quadratically in the positive direction can be written as: $$ f(x) = \left(\tanh\left(x\right)+1\right)\cdot x^{2}+\left(-\tanh\left(x\right)+1\right)\cdot x $$

SeanBrooks
  • 115