1

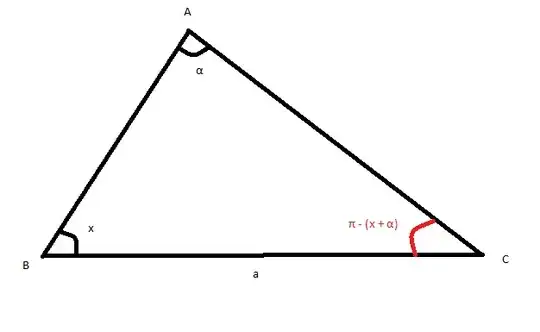
While studying for a test I came across this question. Before approaching I had already found that if there's a triangle $ABC$ with the angle $\angle BAC = \alpha$ (in radians) and the opposite side $BC = a$, then if one of the remaining angles is $x$ ($0<x<\pi -\alpha $) the triangle will have its maximum perimeter when $x = \frac{\pi -\alpha }{2}$. What I did to solve this was finding the maximum perimeter $P_{ABC}$ by creating a function $f\left(x\right)$ and then finding its derivative and thus its maximum value. I show a proposed solution below, but do try solving it before seeing mine. I've already seen some great answers.

Clarification: Since I keep getting suggested a similar question, I would like to clarify that in this proof you don't know that it's an isosceles triangle initially, you have to prove it's an isosceles when it has the maximum perimeter. In the "similar question," you're working all along knowing it's an isosceles triangle and proving it has the maximum perimeter, while here you're proving the triangle to be isosceles knowing it has the maximum perimeter.

Here is what I did: triangle

Here's my proposed solution:

Now I needed to find the other two sides. By the sine law, $$\frac{AB}{\sin \left(\pi -\left(x+\alpha \right)\right)}=\frac{a}{\sin \left(\alpha \right)}$$

$$AB=\frac{a\sin \left(x+\alpha \right)}{\sin \left(\alpha \right)}$$

And

$$\frac{CA}{\sin \left(x\right)}=\frac{a}{\sin \left(\alpha \right)}$$

$$CA=\frac{a\sin \left(x\right)}{\sin \left(\alpha \right)}$$

Now for the function: $$f\left(x\right)=AB\:+BC+CA=\frac{a\sin \left(x+\alpha \right)}{\sin \left(\alpha \right)}+a+\frac{a\sin \left(x\right)}{\sin \left(\alpha \right)} =\frac{a\sin \left(x+\alpha \right)+a\sin \left(\alpha \right)+a\sin \left(x\right)}{\sin \left(\alpha \right)}$$

Rewriting the function and differentiating:

$$f\left(x\right)=\frac{a}{\sin\left(\alpha\right)}\left[\sin\left(x+\alpha\right)+\sin\left(\alpha\right)+\sin\left(x\right)\right]$$

$$f'\left(x\right)=\frac{a}{\sin\left(\alpha\right)}\left[\cos\left(x+\alpha\right)+\cos\left(x\right)\right]$$

$$\cos\left(x+\alpha\right)+\cos\left(x\right)=0$$

$$\cos\left(x+\alpha\right)=-\cos\left(x\right)$$

$$\cos \left(x+\alpha \right)=\cos \left(\pi-x\right)$$

$$x+\alpha =\pi-x$$ $$2x=\pi-\alpha$$ $$x=\frac{\pi-\alpha \:}{2}$$

Now since the last remaining angle is $\pi-\left(x+\alpha\right)$ I will plug in $x=\frac{\pi-\alpha}{2}$ and get $\pi-\left(\frac{\pi-\alpha}{2}+\alpha\right)$ which equals $\frac{\pi-\alpha}{2}$ which is $x$. I have found that the base angles are equal and therefore I have an isosceles triangle.

Hence proved.

libanobovich
  • 129
  • 2
    Right, $x = \pi - (x+\alpha)$ so the $x$ you've found forces the two base angles to be the same i.e. the triangle is isosceles. – Sarvesh Ravichandran Iyer Jun 22 '22 at 08:59
  • For a more "elementary" proof, notice that $\sin x$ is a concave function on $[0,\pi-\alpha]$, so you can use Jensen's inequality on it: $\frac{1}{2}\sin(x)+\frac{1}{2}\sin(\pi-\alpha-x)\le \sin\left(\frac{1}{2}x+\frac{1}{2}(\pi-\alpha-x)\right)=\sin\frac{\pi-\alpha}{2}$, which with Law of sines gives you what you want. –  Jun 22 '22 at 09:37
  • You need to take care with your differentiation - you shouldn't be getting $\sin^2 \alpha$ in the denominator - $\alpha$ is a constant. – Mark Bennet Jun 22 '22 at 09:40
  • @MarkBennet thanks, fixed it. – libanobovich Jun 22 '22 at 10:00
  • @EthanBolker I mean, what you suggested is kind of the opposite of what I asked. I wanted to prove that when the perimeter is maximum the triangle is isosceles, and what you suggested asks to prove that when the triangle is isosceles it has a maximum perimeter. What you suggested is based on the fact that one is, from the beginning, working with an isosceles triangle, while what I asked is to prove that. – libanobovich Jun 22 '22 at 16:24
  • @libanobovich I have removed spoilers from your post. No user ( I believe) is going to work on the problem without seeing your work. Spoilers, IMO, are appropriate only for answers. And that too for only a few lines, not the entire answer. – insipidintegrator Jun 22 '22 at 16:27
  • @insipidintegrator Very well, I will accept the edits. – libanobovich Jun 22 '22 at 16:28

1 Answers1

0

enter image description here

I propose another method; I have chosen this system because if we fix the side DB as a chord and move the point C on the major (or minor; only that C must remain on the same side of DB) arc of the circumcircle, then $\angle DCB$ is fixed for all C.

Let A be the centre of the circle. Let $\angle DCA = \theta$ so that $\angle BCA = \alpha - \theta$.
This gives, by elementary trigonometry, $$CD = 2R\cos\theta, BC=2R\cos(\alpha-\theta)$$ where $R$ is the radius of the circumcircle of $\Delta BDC$.
Now, since side DB (a) is fixed, we must only maximise $$BC+DC=2R(\cos(\alpha-\theta)+\cos\theta) = 2R(2\cos\frac{\alpha}{2}\cos\left(\frac{\alpha}{2}-\theta\right))$$ which happens when $\frac{\alpha}{2}-\theta=0$ (for $\cos x = 1,x=2n\pi$) so $\theta=\frac{\alpha}{2}$.
Now you can prove $\Delta BDC$ to be isosceles by congruence of $\Delta ACF$ and $\Delta ACE$.

insipidintegrator
  • 6,642
  • Neat solution, and of course if you were to work my way: $$f\left(x\right)=2R\left(\cos\left(\alpha-\theta\right)+\cos\left(\theta\right)\right)$$ So $$f'\left(x\right)=2R\left(-\sin\left(\alpha:-\theta:\right)-\sin\left(\theta\right)\right)$$ Using negative angle identity: $$f'\left(x\right)=2R\left(\sin\left(\alpha:+\theta:\right)+\sin\left(-\theta\right)\right)$$ So that $$\sin\left(\alpha:+\theta:\right)=-\sin\left(-\theta\right)$$ $$\sin\left(\alpha:+\theta:\right)=\sin\left(\theta\right)$$ So $$\alpha+\theta =\pi-\theta$$ $$2\theta=\pi-\alpha$$ $$\theta=\frac{\pi-\alpha }{2}$$ – libanobovich Jun 25 '22 at 16:45