From this question post and this youtube video "proof", I am convince that for $x>0$ and $y>0$, the following holds true: $$ \tan^{-1}(x)-\tan^{-1}(y)=\tan^{-1}\left(\frac{x-y}{1+xy}\right)\ \Longleftarrow (Eq.1) $$ Let $x=\frac{w}{w-a}$ and $y=\frac{w}{w+a}$
Substituting into Eq.1 and simplifying yields: $$ \tan^{-1}\left(\frac{w}{w-a}\right)-\tan^{-1}\left(\frac{w}{w+a}\right)=\tan^{-1}\left(\frac{2aw}{2w^{2}-a^{2}}\right)\ \Longleftarrow (Eq.2) $$
When I 3d plot the LHS and RHS of Eq.2, with w and a respectively on x and y axis, I expect the 2 surfaces should overlap at all value. However, it doesn't. The question is why don't they overlap (equal to each other for all value)?
[
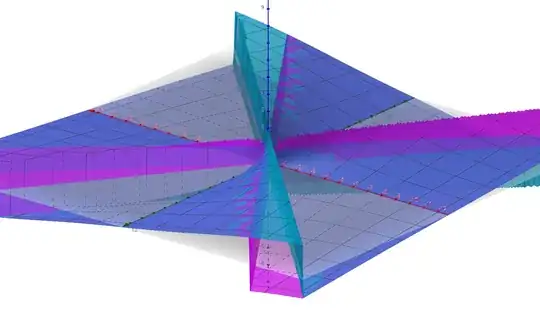The blue is LHS and magenta is RHS.
Edit:
As suggested bym @emacsdrivesmenuts, I'm including the plot for blue minus magenta:
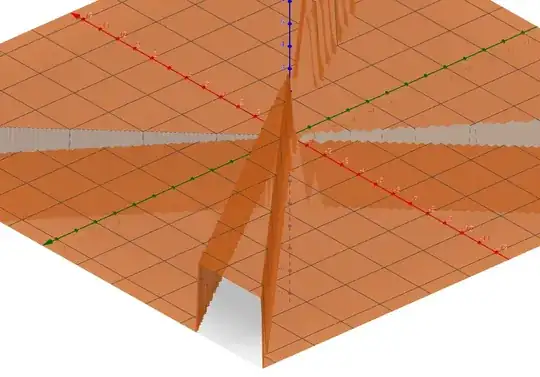The plot suggest that indeed, it holds true for w>a.
