Reference Request - Who originally transformed $ax^2+bxy+cy^2+dx+ey+f=0$ into $X^2+DY^2=N$?

Question

I'm looking for the classical results which gives a transformation of the quadratic $$ax^2 +b xy + cy^2 +dx +ey +f =0$$ into an equation of the form $$ X^2+DY^2 = N$$ I believe it was Lagrange who originally did it, but I can't seem to find it anywhere.

Answer 1

can't imagine this can be traced to one source. On the other hand, there has been some attention to diagonalizing forms, in some quadratic forms book I have. On that note, you may just make $H$ the Hessian matrix of homogenized
$ax^2 + bxy + c y^2 +dxz +eyz +fz^2$ and then, by repeated completing the square, construct nonsingular $P$ such that $P^T HP = D$ is diagonal.

Meanwhile:

When $a \neq 0$ and $ \delta = 4ac - b^2$ and

$g=ax^2 + bxy + c y^2 +dx +ey +f$

If $a=0$ but $c \neq 0$ switch $(x,y)$ so the new $a$ is nonzero.

Here we also use $\delta \neq 0$ For the revised constant term

$ w=(16fc - 4e^2)a^2 + (-4fb^2 + 4edb - 4d^2c)a$

we reach $$ 4a \delta g = ( \delta y + 2ae - bd)^2 + \delta( 2ax + by + d )^2 + w $$

With $g=0$ the right hand side is also $0.$ This way, if everything begins as integers, the final expression is all integers.

Answer 2

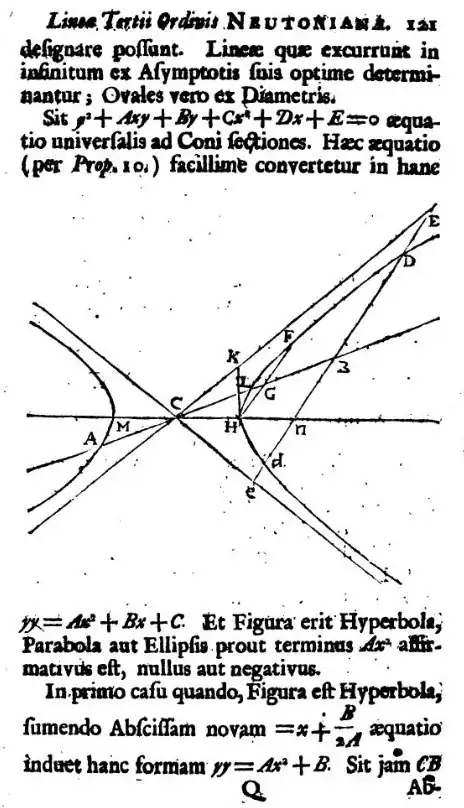
Credit could arguably go to Stirling in his Lineae tertii ordinis Newtonianae (1717). Quoting from Carl Boyer's reputable History of Analytic Geometry (1956):

One of the important additions in Stirling's work is the formal analytic treatment of general second-degree equations. Ever since the time of Descartes geometers had given indications of how to transform the equations of conics to normal forms, and Wallis had asserted that from the coefficients of the equations alone one could determine the characteristics of the curves. De Witt, Craig, L'Hospital, and Wolff had shown how to determine the shape and position of a conic from its equation; but Stirling was perhaps the first one to complete in analytic detail the program of reducing the general quadratic to canonical forms. [...] This was not really new, for similar work along these lines had been given frequently in the seventeenth century; but Stirling went further and calculated analytically from these forms the characteristic properties of the conics with respect to axes, vertices, asymptotes, and parameter -aspects which previous writers had derived geometrically or had taken over from Apollonius.

For reference, this is the original of the relevant (starting) page: