1

I am searching for a tangent (or just it's angle) to an ellipse at a specific point on the ellipse (or it's angle to the center of the ellipse).

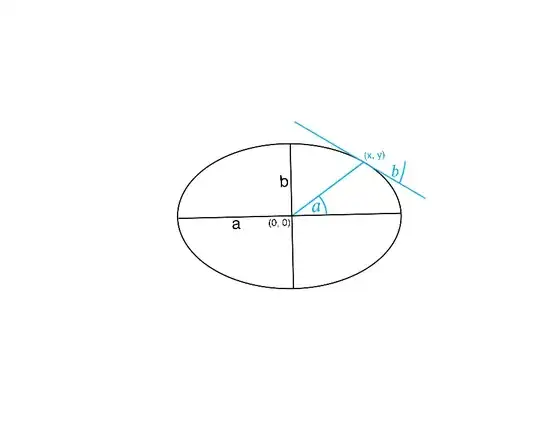
The equation of the ellipse is $\frac{x^2}{\text{a}^2} + \frac{y^2}{\text{b}^2} = 1$. sketch of ellipse

a, b, $a$ and the point of the intersection are given and I search for $b$, the angle of the tangent.

I tried a geometic approach which results a almost accurate angle. I just take a line at two points, one degree left and right to and recieve the angle by using the arc tan of the points.

Is there a more accurate way?

Robert Lee
  • 7,233
Jerry
  • 121
  • Provided $(x_0,y_0)$ is on the ellipse, i.e. $\frac{x_0^2}{\text{a}^2} + \frac{y_0^2}{\text{b}^2} - 1 = 0,$ look at the translation $\frac{(x+x_0)^2}{\text{a}^2} + \frac{(y+y_0)^2}{\text{b}^2} - 1 = 0$ which expands to $(x_0^2/a^2+y_0^2/b^2-1)+x^2/a^2+y^2/b^2+(2yy_0)/b^2+(2xx_0)/a^2=0.$ The tangent cone then is $(2yy_0)/b^2+(2xx_0)/a^2=0$ which translated back is $(2(y-y_0)y_0)/b^2+(2(x-x_0)x_0)/a^2=0$ or $y-y_0=-\frac{x_0}{y_0}\frac{b^2}{a^2}(x-x_0).$ – Jan-Magnus Økland Jan 23 '23 at 07:23

2 Answers2

3

The slope of the tangent to the ellipse at a point is just the derivative. Using implicit differentiation we get that $$ \frac{2x}{a^2} + \frac{2y}{b^2} \frac{\mathrm{d}y}{\mathrm{d}x} = 0 \implies\frac{\mathrm{d}y}{\mathrm{d}x} = -\frac{xb^2}{ya^2} $$ And recalling the point-slope formula for a line, if $(x_0, y_0)$ is some point on the ellipse, then the tangent line at that point is $$ y = -\frac{x_0b^2}{y_0a^2}(x-x_0) + y_0 $$

Robert Lee
  • 7,233
2

Use implicit differentiation.

$$\frac{x^2}{\text{a}^2} + \frac{y^2}{\text{b}^2} = 1$$ $$\frac{2x}{a^2} + \frac{2yy'}{b^2} = 0$$ $$\frac{2b^2x + 2a^2yy'}{a^2b^2} = 0$$ $$2b^2x + 2a^2yy' = 0$$ $$2a^2yy' = -2b^2x$$ $$y' = \frac{-2b^2x}{2a^2y}$$ $$y' = \frac{-b^2x}{a^2y}$$

That gives you the slope of the tangent line at the point $(x, y)$.

Dan
  • 14,978