5

I came up with this construction for $\sqrt{3}$, and want to know if it's valid.

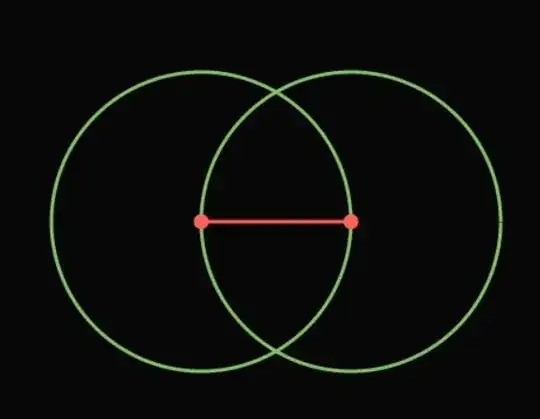
Start with a unit segment $AB$. At points $A$ and $B$, draw two circles with radius 1 like so: enter image description here

Then, mark the points where these circles intersect as $C$ and $D$. Draw line $CD$ between the points. The length of line $CD$ should be precisely $\sqrt{3}$. I think this is so because by the Pythagorean theorem, the height of a triangle drawn between points $A$, $C$, and $B$ should be $\frac{\sqrt{3}}{2}$. Since the length of segment $CD$ should be twice that, and thus $\sqrt{3}$. Is my thinking correct here?

zenzicubic
  • 399

1 Answers1

1

Note that AB is crossed by CD exactly in the middle and vice versa. Assuming that E is the midpoint of A and B, therefore midpoint of C and D, the triangle ACE is rectangle, AC is unit segment, AE is half-unit segment ($AE=AB/2$) and $CE=CD/2$.

$AC^2=AE^2+CE^2 \implies 1^2=(1/2)^2+(CD/2)^2 \implies CD=\sqrt{3}$.

Emerald Moon
  • 26