Can a function have equal maximum and minimum value?

Question

When I heard that the maximum value can be smaller than the minimum value, it striked me whether they can both be equal. I want to enquire whether it is true.

Answer 1

(A) $\bf 1$ Variable function :

It is possible that (minima $\leq$ maxima) OR (minima $>$ maxima), though these will be a different points on the curve.
Pictorially, we can see that here :

In the above graph as you can see, we have a minima at point $A$ and for each of the $3$ different purple curves, we have a point $B$ where $\bf \text{Maxima}>\text{or}=\text{or}<\text{Minima}$ (from top to bottom respectively).

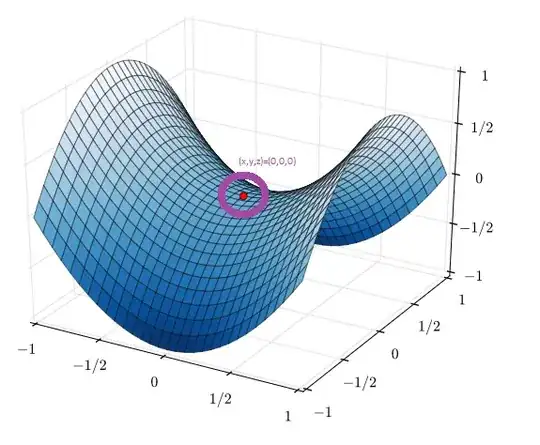
(B) $\bf 2$ Variable functions :

In this case, in addition to earlier cases, it is possible that the same point is both a Minima & a Maxima!
Consider the following function: $$\bf z=x^2-y^2$$ At $(x,y)=(0,0)$ , we have $z=0$ which is a minima when considering Variable $\bf x$ & a maxima when considering variable $\bf y$.
Such Points are known as "Saddle Points" or "MiniMax Points" (more details here) & are very common.

Answer 2

If there are several local maxima and local minima then one local max being less than one local min is ordinary.

However, in case $f(x)$ has single local max and single local min, then the situation of $f_{max}\le f_{min}$ is more interesting as it implies that there is a discontinuity in the function in $(x_{max}, x_{min})$. For example:

$f(x)=\frac{(x-2)^2}{x-3}$, $f_{max}=f(2)=0$ and $f_{min}=f(4)=4$ see below

EDIT An example for $f_{max}=f_{min}$ $$f(x\le 0)=1-(x+2)^2, f(x>0)=1+(x+2)^2$$ as below

Answer 3

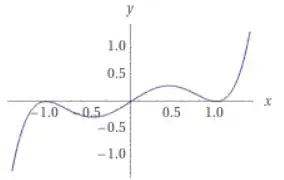
If you're talking about local maxima and minima, then it's definitely possible. As a simple example, check out $y = x (x-1)^2 (x+1)^2$:

This has a local minimum at $(1, 0)$ and a local maximum at $(-1, 0)$, in addition to its two other extrema.