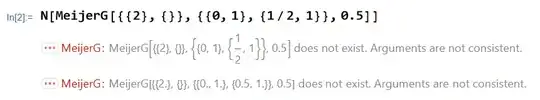The Meijer G function $G^{m,n}_{p,q}\left(\begin{matrix}(a_1,\dots,a_p) \\ (b_1,\dots ,b_q)\end{matrix}\bigg|~z\right)$ is defined via a certain contour integral in the complex plane. In this definition, it is stated that for $k\in\{1,\dots,n\}$ and $j\in\{1,\dots,m\}$, that $a_k-b_j$ cannot be a positive integer, as that would cause the poles in the integrand to coincide.
But, this doesn't seem to stop Mathematica from evaluating it. For instance, when writing this question I was dealing with $$G^{2,1}_{1,4}\left(\begin{matrix} (1) \\ (0,1,\frac{1}{2},1)\end{matrix}\bigg|~z\right)$$ We see clearly that $a_1-b_1=1$ which is a positive integer. So, this instance of the Meijer G shouldn't be defined, according to DLMF and Wikipedia. But my version of Mathematica has absolutely no problems with it, see:
This appears to me like some sort of analytic continuation. For instance, in the original definition of the Riemann zeta function, $\zeta(-1)$ should not be defined (it is a divergent sum). But using the functional equation $$\zeta(1-s)=2\Gamma(s)(2\pi)^{-s}\cos(\pi s/2)\zeta(s)$$ We can obtain $\zeta(-1)=-1/12$.
Is something similar happening with the Meijer G? If so, what? What continuation formula is Mathematica using?
Or perhaps the poles coinciding is really no big deal and it can be evaluated anyway?
I am very confused. Would appreciate some help.
(I have crossposted this on Mathematica SE as well.)