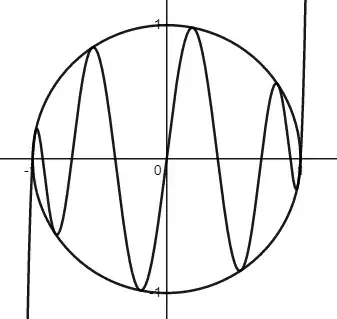
Here is the curve $y=2^{n-1}\prod\limits_{k=0}^n \left(x-\cos{\frac{k\pi}{n}}\right)$, shown with example $n=8$, together with the unit circle centred at the origin.
Call the arc lengths between neighboring roots $l_1, l_2, l_3, ..., l_n$.
What is the exact value of $L=\lim\limits_{n\to\infty}\prod\limits_{k=1}^n l_k$ ?
Desmos suggests that $L$ exists and is approximately $2.94$. Maybe $\frac{8}{e}$ ?
Context
I have studied this curve, and found that it has several interesting properties.
The curve is tangent to the unit circle at $n$ points, which are uniformly spaced around the circle.
The magnitude of the gradient at each root inside the circle is $n$; the magnitude of the gradient at $x=\pm1$ is $2n$.
The total area of the regions enclosed by the curve and the x-axis is $1$.
As $n\to\infty$, the volume of revolution of those regions about the x-axis approaches $\frac{1}{2}$ of the volume of the unit sphere, and the volume of revolution of those regions about the y-axis approaches $\frac{1}{\pi}$ of the volume of the unit sphere.
As $n\to\infty$, if the curve is magnified so that the average area of those regions is always $2$, then the product of those areas approaches $4\cosh^2{\left(\frac{\sqrt{\pi^2-8}}{2}\right)}\approx6.18$, as shown here.
I recently discovered that the product of arc lengths between neighboring roots seems to converge to a positive number as $n\to\infty$. Hence, my question.
(If you know any other interesting properties of this curve, feel free to add them in the comments.)
My attempt
The part of the curve inside the circle can be expressed as $y=-\sqrt{1-x^2}\sin{(n\arccos{x})}$. So
$$L=\lim\limits_{n\to\infty}\prod\limits_{k=1}^n \int_{\cos{\frac{k\pi}{n}}}^{\cos{\frac{(k-1)\pi}{n}}}\sqrt{1+\left(n\cos{(n\arccos{x})+\frac{x\sin{(n\arccos{x})}}{\sqrt{1-x^2}}}\right)^2}dx$$
I do not know how to evaluate this limit. I tried taking the log of the product, without success. I tried to approximate each integral as areas of triangles (hoping that that approximation would become equality with the limit) and a rectangle at the bottom, multiplying each triangle's area by $\frac{4}{\pi}$ (which is the ratio of areas under sine or cosine to the area of an inscribed triangle), but that resulted in a different limit.
EDIT
Further numerical analysis strongly suggests that $L=\frac{8}{e}$. I noticed that when $n$ doubles, the ratio of the two products is a certain number (which is close to $1$), and when $n$ is doubled again, the ratio's distance to $1$ is approximately halved. So then I projected that the product indeed approaches $\frac{8}{e}$. (I don't have Mathematica; anyone who has it is welcome to confirm this.)
I have simplified the expression of $L$. Letting $x=\cos{\frac{u}{n}}$, and ignoring the $1$ in the $\sqrt{1+(...)^2}$ (I think this is OK since $n\to\infty$), we get
$$L=\lim\limits_{n\to\infty}\prod\limits_{k=1}^n \int_{k\pi}^{(k-1)\pi}\sqrt{\left(n\cos{u}+(\sin{u})\cot{\frac{u}{n}}\right)^2}\left(-\frac{1}{n}\sin{\frac{u}{n}}\right)du$$
$$\space{}=\lim\limits_{n\to\infty}\prod\limits_{k=1}^n \int_{(k-1)\pi}^{k\pi}\left|(\cos{u})\sin{\frac{u}{n}}+\frac{1}{n}(\sin{u})\cos{\frac{u}{n}}\right|du$$
So why is this equal to $\frac{8}{e}$ ?
\dfrac(which results in mixed-height math, and uneven vertical spacing), I suggest you to use display-style math when appropriate (i.e., use$$...math...$$, not$...math...$). – metamorphy Sep 29 '22 at 09:11