I'm trying to find a closed form formula for the integral below: $$ \int_{-\infty}^{+\infty} [a(x-b)]^2 \cdot erf(\frac{a(x-b)}{\sqrt{2}}) \cdot \frac{1}{\sqrt{2 \pi}} exp(-\frac{1}{2}x^2) dx, $$ where $x$ is real, and $a, b$ are positive real.
I find Formula 6 in Section 4.3 of this table looks related (screenshot below),
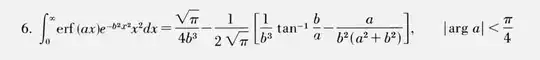 but I'm not sure how to apply a change of variable to get the desired formula, because my integral has a shifted erf. I also found a related post for the product of $x$ with erf and gaussian density here, but it integrates over $(0, +\infty)$ and the most recent answer did not show the steps. What are some techniques that I can try? Thank you!
but I'm not sure how to apply a change of variable to get the desired formula, because my integral has a shifted erf. I also found a related post for the product of $x$ with erf and gaussian density here, but it integrates over $(0, +\infty)$ and the most recent answer did not show the steps. What are some techniques that I can try? Thank you!
Edit: Some attempt of change of variable and integration by parts. Let $y=x-b$, then the integral becomes $$ \frac{1}{\sqrt{2 \pi}} \exp(-\frac{1}{2} b^2) \int_{-\infty}^{+\infty} a^2 y^2 \cdot erf(\frac{ay}{\sqrt{2}}) exp(-\frac{1}{2}y^2) exp(-by) dy. $$ Let $$ u = y^2 \cdot erf(\frac{ay}{\sqrt{2}}) exp(-\frac{1}{2}y^2), dv = exp(-by) dy, $$ then $$ du = [2y \cdot erf(\frac{ay}{\sqrt{2}}) exp(-\frac{1}{2}y^2) + \sqrt{\frac{2}{\pi}} ay^2 exp(-y^2) - y^3 erf(\frac{ay}{\sqrt{2}}) exp(-\frac{1}{2}y^2)] dy, \\ v = -\frac{1}{b} exp(-by). $$ There will be another integral without a known formula in $\int v du$, that is, $$ \int y^3 erf(\frac{ay}{\sqrt{2}}) exp(-\frac{1}{2}y^2) exp(-by) dy. $$