In $\triangle ABC$, $BD$ is a median, $\angle DAB=15$ and $\angle ABD=30$. Find $\angle ACB$.

Question

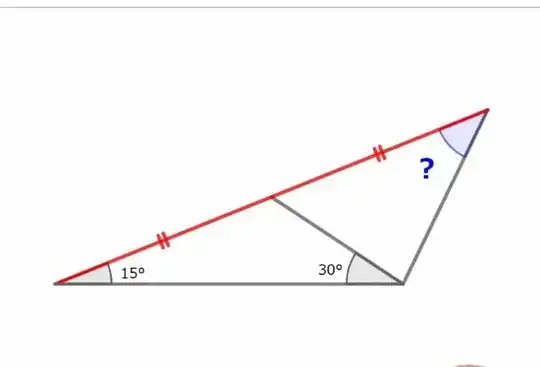
As title implies, the goal is to find the measure of the missing angle in the following figure. While I have solved this, which I'll show below as an answer, I'm not quite sure if my answer is accurate, so I'm posting this here to see if my answer is correct and if there are any alternative approaches. Please post your own approaches to this!

Answer 1

In the figure, $\Delta AED$ together point $C$ constitute the given figure.

The constructions are:

(1) Equilateral triangle $BAC$,

(2) A circle with center $B$ and radius $BA$,

(3) Note that the circle passes through $E$ because $\angle AEC=\frac{\angle ABC}{2}$

(4) Join $DB$

Note that we do not assume that $D, E, B$ are collinear.

We are going to $\color{red}{prove}$ that $\color{red}{D, E, B}$ are $\color{red}{collinear}$.

$\color{red}{Proof:}$

Note that $\angle EAB=45^o$ and $BA=BE \implies \angle ABE=90^o$

i.e. $\color{red}{BE \bot BA}$

On the other hand, $AC=CB=CD \implies \angle ABD=90^o$

i.e. $\color{red}{BD \bot BA}$

The $2$ statements implies that $B, E, D$ are collinear.

Since $CB=CD, \angle BCA=60^o $ and $BCD$ is a trianlge, $\angle CDB=30^0$

Answer 2

This is going to be my approach. I'll add an explanation as well!

Here's how I go about it:

1.) Label the triangle as $\triangle ABC$ where $BD$ is the median with $AD=DC$. Rotate $\triangle ABD$ across median $BD$ such that the new triangle $\triangle EBD$ is congruent to $\triangle ABD$ with $AD=ED=DC$. Since $\angle ABD=\angle EBD=30$, and segment $AB=EB$, we can conclude that $AB=EB=AE$, therefore $\triangle ABE$ is equilateral.

2.) This implies that $\angle EAD=\angle AED=45$. Connect point $E$ and $C$ via $EC$. Notice that since the circumcenter of $\triangle AEC$ lies on $AC$, it follows that $\triangle AEC$ is a right angle triangle. But, since $\angle EAD=45$ and $\angle AEC=90$, this implies that $\angle ECA=45$, therefore $\triangle AEC$ is an isosceles right angle triangle, meaning that $AB=AE=EB=EC$.

3.) Above implies that $E$ is the circumcenter of $\triangle ABC$ (since $E$ is equidistant from all vertices of $\triangle ABC$). This then implies that $\angle ACB$ is half of $\angle AEB$ (inscribed angle theorem). Therefore $\angle ACB=30$.

Answer 3

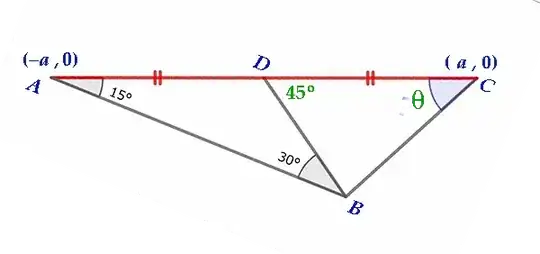
Let $AD=DC=a$ and $DB=b$ according to Goku's figure. Then by law of sines in left and right triangles respectively:

$\frac{a}{\sin30}=\frac{b}{sin15}$ and $\frac{a}{\sin(135-x)}=\frac{b}{sinx}$.

Eliminating $a$ and $b$ we have $\sin15\sin(135-x)=\sin30\sin x$.

After simplifications, we find $\cot x=\frac{\sqrt{2}-\sqrt{2-\sqrt{3}}}{\sqrt{2-\sqrt{3}}}=\sqrt{3}$ and thus $x=30$.

Answer 4

Let $\color{blue}{l=(BD)}$ and $\color{blue}{s=s_l}$ the symetry.

$$s(\angle ABD)=\angle DBE=30°$$ $$s([AB])=[BE]\implies \triangle ABE \text{ isoscele}$$ $$\angle ABE=60°\implies \triangle ABE \text{ equilateral}\implies \angle AEB=60°$$

Then the arguments provided by @Goku[I wonder if I really simplified :) but i love exo]

Answer 5

WLOG, let $AD=DC=1$

Using sine rule yields $$ \begin{aligned} \frac{A B}{\sin 135^{\circ}}&=\frac{1}{\sin 30^{\circ}} \Rightarrow A B =\sqrt{2} \end{aligned} $$ Using cosine rule gives $$ \begin{aligned} BC^2 &=2^2+\sqrt{2}^2-2(2) \sqrt{2} \cos 15^{\circ} \\ &=6-4 \sqrt{2} \cos 15^{\circ} \\ &=6-2(\sqrt{3}+1) \\ B C &=\sqrt{4-2 \sqrt{3}}=\sqrt{3}-1 \end{aligned} $$ By sine rule again, we have $$ \begin{aligned} \frac{\sin C}{A B} &=\frac{\sin 15^{\circ}}{BC} \\ \sin C &=\frac{\sqrt{2} \sin 15^{\circ}}{\sqrt{3}-1}=\frac{\frac{\sqrt{3}-1}{2}}{\sqrt{3}-1}=\frac{1}{2} \\ C &=30^{\circ} \end{aligned} $$

Answer 6

We may choose a coordinate system in which $ \ D \ $ lies at the origin, with vertices $ \ A \ $ and $ \ C \ $ at $ \ (-a \ , \ 0) \ $ and $ \ (a \ , \ 0 ) \ \ , \ $ respectively. It is straightforward to show that $ \ m(\angle BDC) \ = \ 45º \ \ . \ $ Vertex $ \ B \ $ is then the intersection of line $ \ \overrightarrow{AB} \ \ , \ $ with equation $ \ y \ = \ -m·(x + a) \ \ $ (with $ \ m \ = \ \tan 15º \ ) \ $ , and line $ \ \overrightarrow{DB} \ \ , \ $ with equation $ \ y \ = \ -x \ \ . \ $ The coordinates of $ \ B \ $ are found from $$ -mx - ma \ \ = \ \ -x \ \ \Rightarrow \ \ x_B \ \ = \ \ a·\left(\frac{m}{1 - m} \right) \ \ = \ \ -y_B \ \ ; $$ this result is reasonable, since $ \ 0 \ < \ m \ < \ 1 \ \Rightarrow \ -y_B \ < \ 0 \ < \ x_B \ \ . $

Vertex $ \ B \ $ also lies on line $ \ \overrightarrow{CB} \ $ of unknown slope $ \ M \ = \ \tan \theta \ $ through vertex $ \ C \ \ , \ $ so its equation is $ \ y \ = \ M·(x-a) \ \ . \ $ We thus determine $$ -a·\left(\frac{m}{1 - m} \right) \ \ = \ \ M·\left( \ a·\left[\frac{m}{1 - m} \right] - a \right) \ \ \Rightarrow \ \ -ma \ \ = \ \ M · (ma \ - \ a \ + \ ma) $$ $$ \Rightarrow \ \ M \ \ = \ \ \frac{m}{1 \ - \ 2m} \ \ . $$

To be frank, I had hoped that I'd have something that suggested the "double-angle" formula for tangent. Instead, we'll need to apply one of the "half-angle" formulas for tangent to produce $$ m \ \ = \ \ \tan 15º \ \ = \ \ \frac{1 \ - \ \cos 30º}{ \sin 30º } \ \ = \frac{1 \ - \ \frac{\sqrt3}{2}}{ \frac12 } \ \ = \ \ 2 \ - \ \sqrt3 \ \ , \ $$ the result Bob Dobbs applies. It follows immediately that

$$ M \ \ = \ \ \frac{2 \ - \ \sqrt3}{1 \ - \ (4 \ - \ 2\sqrt3)} \ \ = \ \ \frac{2 \ - \ \sqrt3}{2\sqrt3 \ - \ 3} \ \ = \ \ \frac{1}{\sqrt3} \ \ = \ \ \tan 30º \ \ . $$

Hence, $ \ m(\angle DCB) \ = \ \theta \ = \ 30º \ \ . $

[It might be mentioned that this is one of the few slopes for which this "tangent of twice the angle" relation is satisfied: $$ M \ \ = \ \ \tan (2 \theta) \ \ = \ \ \frac{2m}{1 \ - \ m^2} \ \ = \ \ \frac{m}{1 \ - \ 2m} \ \ \Rightarrow \ \ 2m \ - \ 4m^2 \ \ = \ \ m \ - \ m^3 $$ $$ \Rightarrow \ \ m·(m^2 \ - \ 4m \ + \ 1) \ \ = \ \ 0 \ \ \Rightarrow \ \ m \ \ = \ \ 0 \ \ , \ \ 2 \ \pm \ \sqrt3 \ \ . \ ] $$

(Incidentally, in looking for a "Euclidean" proof (which I'll post if I get it sorted out), I noticed that this problem has some points of similarity with one you posted earlier.)