3

Consider a continuous function $f : U \to \mathbb{R}$ where $U \subset \mathbb{R}^{m}$ is a convex compact set.

Also, let $\text{conv} f$ be the (greatest) convex minorant, that is, $\text{conv} f(u) := \sup_{g \in G}g(u)$ where $g \leq f$ and $g$ is convex.

If $f$ has a unique minimum point, then does $g$ have a unique minimum point as well?

+) If $f$ is Lipschitz in addition to the previous conditions, so does $g$?

Jinrae Kim
  • 590
  • 2
    This is tougher than I expected! – copper.hat Nov 07 '22 at 21:01
  • @copper.hat Yeah, I'm telling you! haha For my research of function approximation, I ended up using a detour by slightly changing the original function to make sure that its convex minorant has a unique minimum point as well. The main idea is based on what you suggested. – Jinrae Kim Nov 08 '22 at 05:43
  • 1
    This question has been bothering me since I read it :-). I thought it was trivial, but so far have been unable to make any real progress. – copper.hat Nov 08 '22 at 05:51
  • @copper.hat My guess is, if a given function is bivarating and the value can be arbitrarily close to the minimum, then the minimum point might not be unique. I'm not sure such a function can exist under the requirements though. – Jinrae Kim Nov 08 '22 at 08:40
  • I don't have a strong guess, but I would imagine it remains unique. – copper.hat Nov 08 '22 at 14:45
  • I think the solution for $m=1$ is straightforward. I don't know how to handle $m>1$. – copper.hat Nov 23 '22 at 02:16
  • @copper.hat If you don't mind, could you answer it for m=1? – Jinrae Kim Nov 24 '22 at 03:03
  • I added an answer for general $m$. The idea is straighforward, but awkward to express. – copper.hat Nov 24 '22 at 06:45

1 Answers1

1

Suppose $u^*$ is the minimiser of $f$ on $U$. Let $g(u) = \sup \{ h(u) | h \text{ is convex}, h \le f \}$. Note that $u \mapsto f(u^*)$ is convex and majorised by $f$ hence $g(u) \ge f(u^*)$ for all $u \in U$.

Suppose $u' \in U$ with $u' \neq u$ is such that $g(u') = f(u^*)$. For $r>0$ (and small enough so that $U$ is not completely contained in $B(u^*, r)$), define $m(r) = \min\{ f(u) | u \in U \setminus B(u^*, r) \}$. Note that $m(r) >f(u^*)$ for those $r>0$ for which $m$ is defined.

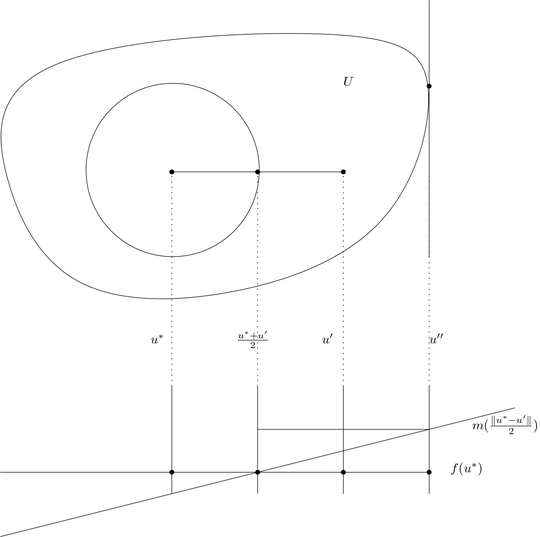
Excuse the giant picture, attempts to scale failed, but having the picture helps understand the construction. enter image description here

Let $d = u'-u$ and $u'' \in \operatorname{argmax}_{u \in U} \langle d, u \rangle$. Define the affine function $a(u) = f(u^*)+\alpha \langle d, u -{1 \over 2}(u^*+u')\rangle $ and $\alpha$ is chosen such that $a(u'') = m({1 \over 2}\|u'-u^*\|))$.

Note that if $u\in U$ is such that $\langle d, u -{1 \over 2}(u^*+u')\rangle \ge 0$ then $u \in U \setminus B(u^*, r)$, where $r = {1 \over 2}\|u'-u^*\|$ and so $f(u) \ge m(r) > f(u^*)$. Hence $a$ is majorised by $f$ and since $g(u') \ge a(u') > f(u^*)$ we obtain a contradiction.

Hence no such $u'$ exists.

copper.hat
  • 172,524
  • Thanks for your answer. I'm a bit confused; what is $g$ here? I mean, why does the fact that $u \mapsto f(u^{*})$ is majorised by $f$ imply $g \geq f$? – Jinrae Kim Nov 25 '22 at 22:15
  • 1
    $g$ is the greatest convex minorant. – copper.hat Nov 25 '22 at 22:32
  • Why the downvote? If there is something wrong please let me know so it can be repaired. – copper.hat Nov 27 '22 at 14:32
  • 1
    It's weird. I didn't. I actually didn't take a look at it in details yet because of Thanksgiving. Can anyone who downvoted let us know if there is something wrong? – Jinrae Kim Nov 28 '22 at 03:19
  • 1
    @JinraeKim I had a small error in the definition of $d$. If we let $l(u)= \langle d, u -{1 \over 2}(u^+u')\rangle$, note that $l({1 \over 2}(u^+u')) = 0$ and $l(u')= {1 \over 2} |d|^2 >0$, so you can always choose $\alpha>0$ such that the above constraint on $a(u'')$ holds. – copper.hat Nov 28 '22 at 03:39
  • The construction is so that $f(u) \ge a(u) $ for all $u$, $f$ majorises the affine (hence convex) $a$. The epigraph of $f$ lies above the slanted line above (which is meant to depict $a$). – copper.hat Nov 28 '22 at 03:40
  • Ah! Now I see. This seems pretty nice to me! To clarify your answer for future readers, i) if the inner product is less than zero for some $u \in U$, then it is less than the minimum value of f, $f(u^{})$; for those $u \in U$, $a(u)$ is less than $f(u)$. And ii) if the inner product is greater than or equal to zero for some $u \in U$, then it should be in $u \in U \ B(u^{}, r)$ (think about it for a bit!) and by the definition of $u''$, $a(u)$ is at most $m(r)$; therefore, $a(u)$ is less than $f(u)$ again for those $u$'s. Therefore, the convex function $a$ is majorised by $f$. – Jinrae Kim Nov 28 '22 at 06:15
  • 1
    I think that we can conclude the proof by showing that $g$ has the unique minimum at $u^{}$ with the minimum value of $f(u^{})$; this is trivial from the fact that the definition of $\text{conv} f$ in the original question corresponds to the pointwise-minimum convex function, which implies that $g(u^{}) = f(u^{})$ from that the constant function $u \mapsto f(u^{*})$ is convex and majorised by $f$. – Jinrae Kim Nov 28 '22 at 06:19
  • @JinraeKim Thanks, your last two comments look good to me. – copper.hat Nov 28 '22 at 06:21