18

Martin Gardner, somewhere in the book Mathematical Carnival; talks about superellipses and their application in city designs and other areas. Superellipses(thanks for the link anorton) are defined by the points lying on the set of curves:

$$\left|\frac{x}{a} \right|^n + \left|\frac{y}{b} \right|^n = 1$$

After reading the chapter, I was wondering how to calculate the area of these shapes. So I started by the more simplistic version of supercircles' area:

$$\frac{A}{4}=\int_0^1 \sqrt[n]{1-x^n}dx$$

Although, it looks simple, but I wasn't able to evaluate the integral(except some simple cases, i.e. $n=1,2,\frac{1}{2},\frac{1}{3},\cdots$). So I asked Mathematica to see if its result can shed some light on the integration procedure, the result was:

$$\int_0^1\sqrt[n]{1-x^n}dx=\frac{\Gamma \left(1+\frac{1}{n}\right)^2}{\Gamma \left(\frac{n+2}{n}\right)}$$ where $\Re(n)>0$. But I still couldn't figure out the integration steps. So my question is: how should we do this integration?

SideNotes:

It's easy to evaluate the integral in the limit of $n \rightarrow \infty$! One way to do it is using Taylor series expansion, and keeping the relevant terms(only first term in this case).

Some beautiful supercircles are shown in the image bellow:

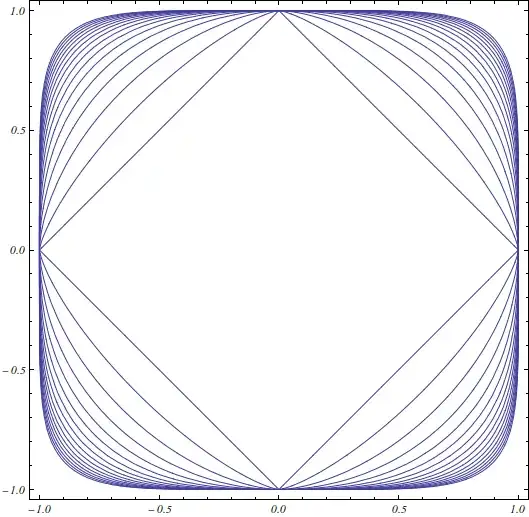
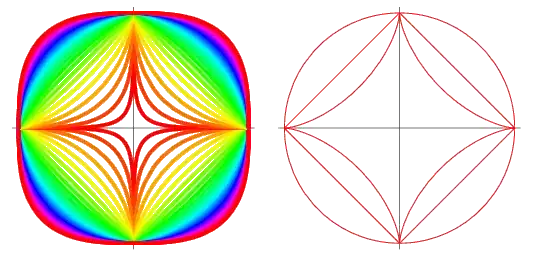
supercircles beautiful supercircles

As one can see their limiting case is a square.

Also, it will be really nice, if one can calculate the volume of the natural generalization of the curve to 3(or $k$) dimensions:

$$\left|\frac{x}{a} \right|^n + \left|\frac{y}{b} \right|^n +\left|\frac{z}{c} \right|^n = 1$$

Zacky
  • 27,674
Ali
  • 1,399
  • 3
    This page gives a parametrization for the bounding curve... it could be that Green's Thm would produce the area, but I haven't worked it out yet. – apnorton Aug 03 '13 at 13:39
  • @anorton That was an interesting link(with some beautiful curves)! – Ali Aug 03 '13 at 13:43
  • 1
    It might also be mentioned that these are the unit balls of the $L^p$ norms in $R^2$. – abnry Aug 03 '13 at 15:10
  • Please don't bump old question just to add a "mathrm" for $dx$, or atleast add it everywhere on the post not only for the title. In the end this is just a style preference, it doesn't add anything essential to the post and maybe should be left at OP's choice. – Zacky Dec 22 '19 at 19:51
  • 1
    @Zacky Since I added a new answer so this question gets bumped either way. However, you are right that I forgot to apply my "cosmetic" change also to the question body... Well I guess it will just stay like this now – Maximilian Janisch Dec 22 '19 at 19:56

3 Answers3

15

Let $t=x^n$, hence $dt = nx^{n-1}dx = nt^{1-\frac{1}{n}}dx$ \begin{align*} \int_0^1 \sqrt[n]{1-x^n}dx&=\frac{1}{n}\int_0^1t^{\frac{1}{n}-1}(1-t)^{\frac{1}{n}} dt\\ &=\frac{1}{n}\int_0^1t^{\frac{1}{n}-1}(1-t)^{1 + \frac{1}{n} - 1} dt\\ &=\frac{1}{n}\beta\biggr(\frac{1}{n}, 1+\frac{1}{n}\biggr)\\ &=\frac{1}{n}\frac{\Gamma(\frac{1}{n})\Gamma(1+\frac{1}{n})}{\Gamma(\frac{n+2}{n})}\\ &=\frac{\Gamma(1+\frac{1}{n})^2}{\Gamma(\frac{n+2}{n})} \end{align*}

Wonderful problem presentation by the way! I enjoyed waking up to this.

A.E
  • 2,473
8

Hint: Use the change of variables $t=x^{n}$ and then use the $\beta$ function

$$ \mathrm{\beta}(u,v) = \int_0^1 t^{u-1}(1-t)^{v-1}\,dt=\frac{\Gamma(u)\Gamma(v)}{\Gamma(u+v)},\quad \textrm{Re}(u), \textrm{Re}(v) > 0.\, $$

Mhenni Benghorbal
  • 47,431
2

We can compute an anti-derivative of $\sqrt[k]{1-x^k}$:

For any $y\in[0,1]$ and $k\in]0,\infty[$, \begin{split} \int_0^y \sqrt[k]{1-x^k}\,\mathrm dx&\overset{u=x^k}= \frac1k\int_0^{y^k} u^{\frac1k-1} \cdot (1-u)^{\frac1k}\,\mathrm du\\ &=\frac1k\cdot\operatorname B_{y^k}\left(\frac1k,\frac1k+1\right)\\ &=y\cdot{}_2F_1\left(-\frac1k,\frac1k;1+\frac1k;y^k\right), \end{split}

where $\operatorname B$ denotes the Incomplete Beta Function and ${}_2F_1$ is the Gaussian hypergeometric function. The last equality is proven here.

Hence, we have on $[0,1]$, where $c$ is an integration constant, $$\bbox[5px,border:2px solid #C0A000]{\int\sqrt[k]{1-x^k}\,\mathrm dx=\frac1k\cdot\operatorname B_{x^k}\left(\frac1k,\frac1k+1\right)+c=x\cdot{}_2F_1\left(-\frac1k,\frac1k;1+\frac1k;x^k\right)+c.}$$

In particular, by the Fundamental Theorem of calculus, where $\Gamma$ denotes the Gamma function, $$\bbox[5px,border:2px solid #C0A000]{\int_0^1\sqrt[k]{1-x^k}\,\mathrm dx={}_2F_1\left(-\frac1k,\frac1k;1+\frac1k;1\right)=\frac{\Gamma \left(1+\frac{1}{k}\right)^2}{\Gamma \left(\frac{k+2}{k}\right)}=\frac{\sqrt{\pi }}{4^\frac1k}\frac{\Gamma \left(1+\frac{1}{k}\right)}{\Gamma \left(\frac{1}{2}+\frac{1}{k}\right)},}$$

where the second last equality is Gauss's Hypergeometric Theorem and the last equality is the Gamma function–Legendre formula.

Maximilian Janisch
  • 13,536
  • 1
    I will suggest to add some ";" for the Hypergeometric function. In particular for $_2F_1\left(a,b\color{red};c\color{red};x\right)$ the first two terms, $a$ and $b$, are meant two denote the two rising factorials on the numerator and $c$ denotes the one from the denominator, the last term is simply a parameter. Those are split in the $F$ function by a semicolon. – Zacky Dec 22 '19 at 20:28
  • 1
    @Zacky Thanks, done. I probably forgot them because I was excited that there is a closed form of this integral (a friend asked me about this integral and I only found this MSE question after already having written the above text) – Maximilian Janisch Dec 22 '19 at 20:30